Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình xin làm bài 2 thôi.
Bài 2:
a/ Ta có tam giác ABC cân tại A => AM vừa là trung tuyến vừa là đường cao
=> AM \(⊥\)BC
b/ Ta có M là trung điểm BC => BM = CM = 1/2 BC = 1/2 x 3 = 1,5 (cm)
Xét tam giác ABM vuông tại M có:
\(AM^2+BM^2=AB^2\left(pytago\right)\)
\(AM^2+1,5^2=5^2\)
\(AM^2+2,25=25\)
\(AM^2=22,75\Rightarrow AM=\sqrt{22,75}\approx4,8\left(cm\right)\)
PS: Câu b bạn dùng pytago với tam giác bên kia cũng dc nha

a.Ta có: AB=AC ( gt )
=> Tam giác ABC cân tại A
Mà AM là đường trung tuyến => AM cũng là đường cao
=> AM vuông góc với BC
b. Ta có: BH = BC : 2 ( AM là đường trung tuyến )
=> BH = 32 : 2 = 16cm
Áp dụng định lý pitago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM=\sqrt{AB^2-BM^2}=\sqrt{34^2-16^2}=\sqrt{900}=30cm\)
c.Xét tam giác vuông BMF và tam giác vuông CME, có:
góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy tam giác vuông BMF = tam giác vuông CME ( cạnh huyền. góc nhọn)
=> BF = CE ( 2 cạnh tương ứng )
=> AF = AE ( AB = AC; BF = CE )
=> Tam giác AEF cân tại A
=> AM vuông với EF (1)
Mà AM cũng vuông với BC (2)
Từ (1) và (2) suy ra EF//BC
d. ta có: BM = CM ( gt ) (3)
Mà trong tam giác vuông MCE có ME là cạnh huyền
=> \(ME>MC\) (4)
Từ (3) và (4) suy ra \(ME>MB\)

a: Ta có:ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: BM=CM=BC/2=16cm
=>AM=30(cm)
c: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
\(\widehat{FAM}=\widehat{EAM}\)
Do đó: ΔAFM=ΔAEM
Suy ra: AF=AE
Xét ΔABC có AF/AB=AE/AC
nên FE//BC

a.Ta có: AM là đường trung tuyến trong tam giác cân ABC
=> Cũng là đường cao
=> AM vuông góc với BC
b.Có AM là đường trung tuyến \(\Rightarrow BM=BC:2=32:2=16cm\)
Áp dụng định lý pytago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM^2=34^2-16^2\)
\(AM=\sqrt{900}=30cm\)

Đề thiếu yêu cầu hay là thừa dữ kiện? Thực sự cm \(AM⊥BC\)không cần đến độ dài cạnh. Cần \(\Delta\)cân và 1 đường (ở đây là trung tuyến) là đủ!
(Bạn tự vẽ hình nhé!)
Ta có: \(\Delta ABC\)cân tại \(A\Rightarrow AM\)vừa là trung tuyến vừa là đường cao \(\Rightarrow AM⊥BC\)
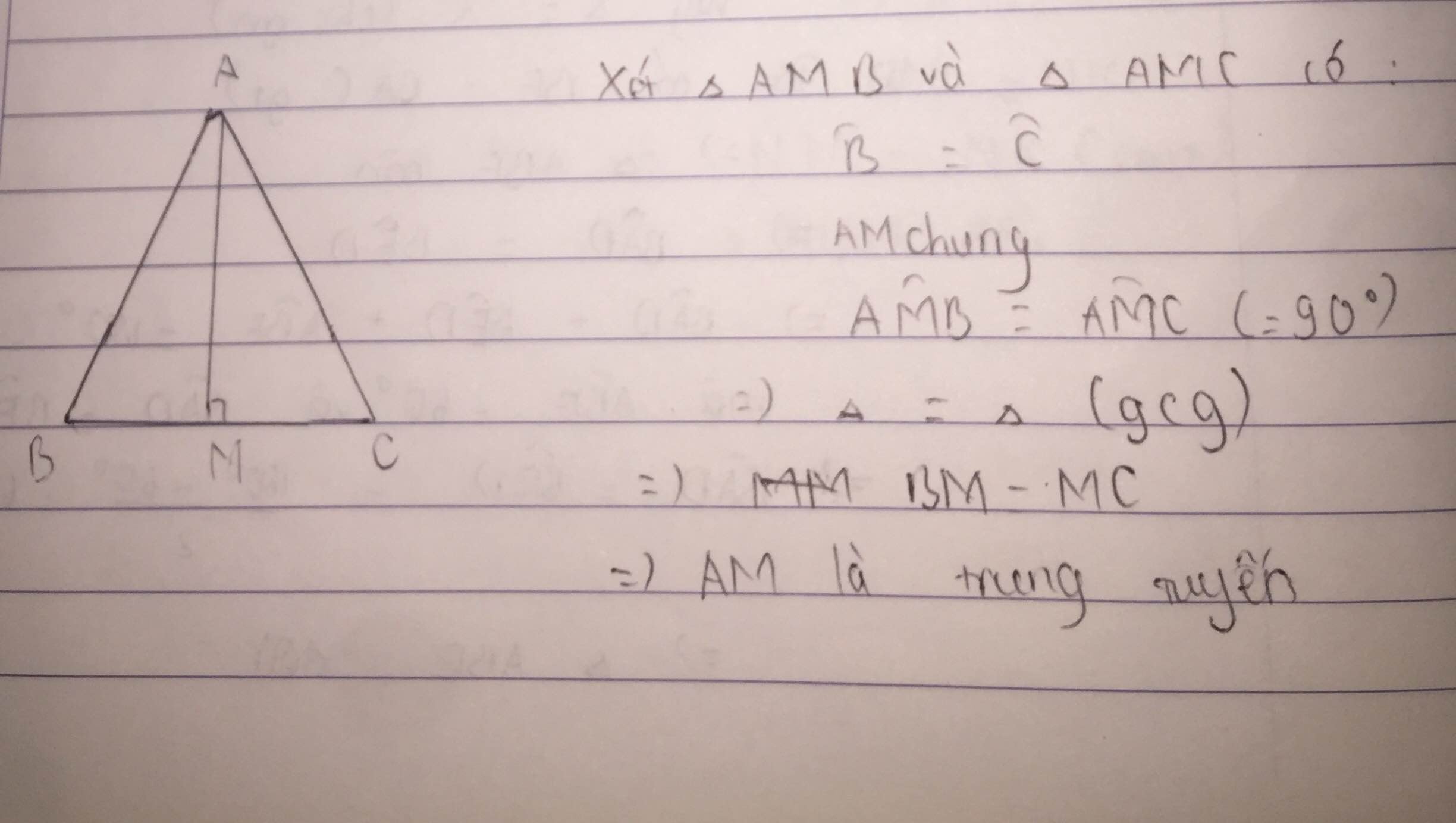
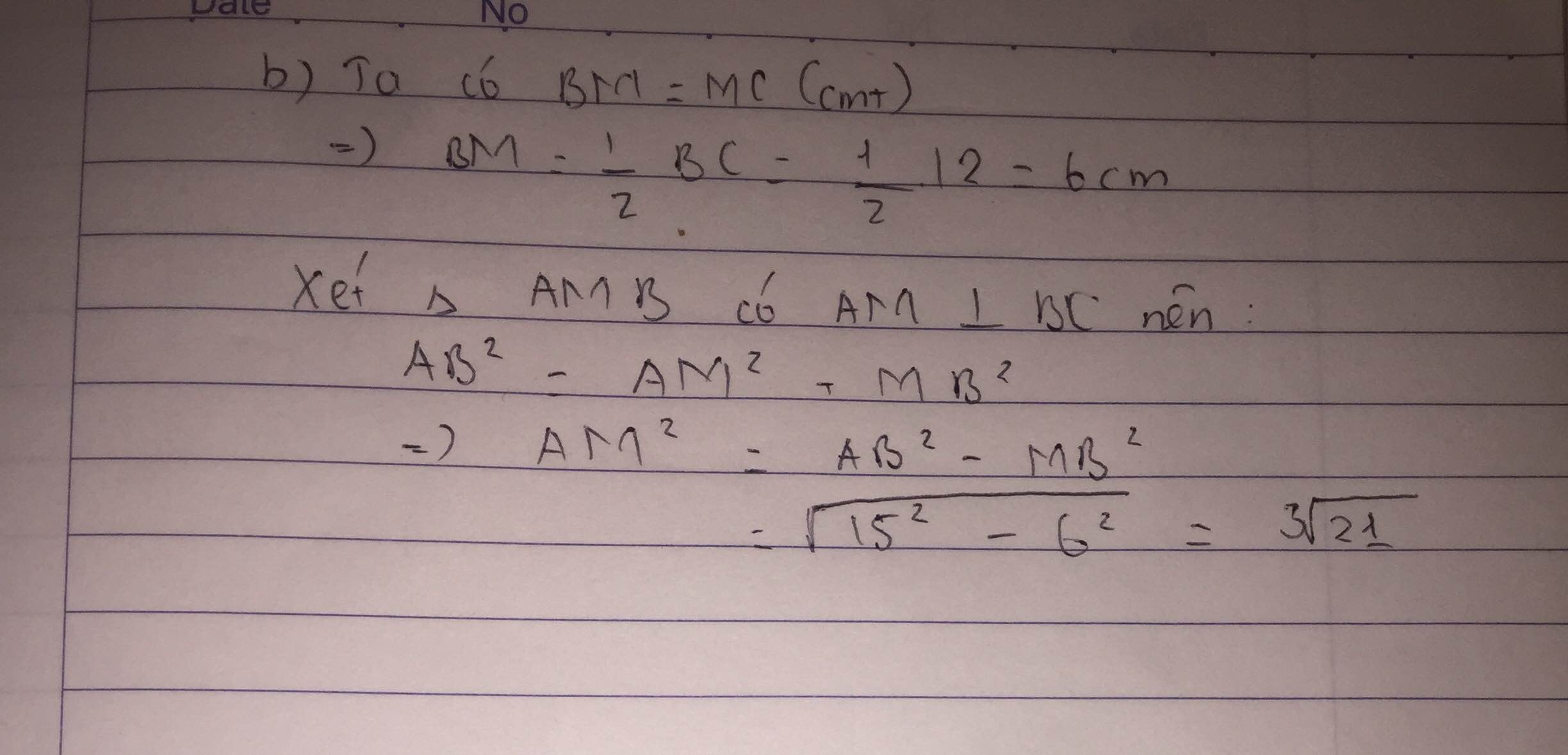
a, Xét tam giác ABC cân tại A có AM là trung tuyến
=> AM đồng thời là đường cao => AM vuông BC
b, Ta có BM = BC/2 = 3/2 cm
Theo định lí Pytago tam giác AMB vuông tại M
\(AM=\sqrt{AB^2-BM^2}=\dfrac{\sqrt{91}}{2}cm\)