Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là trọng tâm tam giác ABC
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1}{3};y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{1}{3}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất khi \(3MG\) nhỏ nhất
\(\Leftrightarrow M\) là hình chiếu của \(G\) trên trục tung
\(\Leftrightarrow M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\le3MG=1\)
Đẳng thức xảy ra khi \(M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\) Tung độ \(y_M=\dfrac{1}{3}\)

Chọn D.
Gọi điểm M có tọa độ là ( x; y)
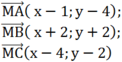
MA2 + 2MB2 + 3MC2
= (x - 1)2 + (y - 4)2 + 2[ (x + 2)2 + (y + 2)2] + 3[ (x - 4)2 + (y - 2)2]
= 6x2-18x + 6y2 + 93 = 1,5. (2x - 3)2 + 6(y - 1)2 + 147/2 ≥ 147/2
Dấu “=” xảy ra khi x = 1,5 và y = 1
Vậy tọa độ điểm M cần tìm là ( 1,5; 1).

\(\overrightarrow{AB}=\left(-1;1\right)\) nên pt AB có dạng:
\(1\left(x-2\right)+1\left(y-3\right)=0\Leftrightarrow x+y-5=0\)
Do I thuộc AB nên tọa độ có dạng: \(I\left(a;5-a\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{IA}=\left(2-a;a-2\right)\\\overrightarrow{IB}=\left(1-a;a-1\right)\\\overrightarrow{IC}=\left(-1-a;a-10\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}=\left(-9a;9a-55\right)\)
\(\Rightarrow\left|\overrightarrow{IA}+3\overrightarrow{IB}+5\overrightarrow{IC}\right|=\sqrt{\left(9a\right)^2+\left(55-9a\right)^2}\ge\sqrt{\dfrac{1}{2}\left(9a+55-9a\right)^2}=\dfrac{55}{\sqrt{2}}\)
Dấu "=" xảy ra khi \(9a=55-9a\Rightarrow a=\dfrac{55}{18}\Rightarrow I\left(\dfrac{55}{18};\dfrac{35}{18}\right)\)
Kiểm tra lại tính toán

Do E thuộc Ox nên tọa độ có dạng: \(E\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{EM}=\left(1-x;-2\right)\\\overrightarrow{EN}=\left(3-x;2\right)\\\overrightarrow{EP}=\left(5-x;-1\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}=\left(9-3x;-1\right)\)
\(\Rightarrow\left|\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}\right|=\sqrt{\left(9-3x\right)^2+\left(-1\right)^2}\ge1\)
Dấu "=" xảy ra khi \(9-3x=0\Rightarrow x=3\Rightarrow E\left(3;0\right)\)

Gọi \(M\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-x;1\right)\\\overrightarrow{MB}=\left(1-x;3\right)\\\overrightarrow{MC}=\left(-2-x;2\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\left(-2x+4;5\right)\)
\(\left|\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\right|=\sqrt{\left(-2x+4\right)^2+5}\ge\sqrt{5}\)
Dấu "=" xảy ra khi \(-2x+4=0\Leftrightarrow x=2\Rightarrow M\left(2;0\right)\)