Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tại sao
Q=\(2\sqrt{\left(9-3m\right)^2}...\)
chuyển xuống thành \(\sqrt{\left(18-6m\right)^2...}\)
sao không phải là nhân 4 ở trong mài
vì \(2=\sqrt{4}\), vậy thì phải nhân 4 chứ
Do M thuộc Ox, gọi tọa độ M có dạng \(M\left(m;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-m;-4\right)\\\overrightarrow{MB}=\left(4-m;5\right)\\\overrightarrow{MC}=\left(-m;-9\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+2\overrightarrow{MB}=\left(9-3m;6\right)\\\overrightarrow{MB}+\overrightarrow{MC}=\left(4-2m;-4\right)\end{matrix}\right.\)
\(Q=2\sqrt{\left(9-3m\right)^2+6^2}+3\sqrt{\left(4-2m\right)^2+\left(-4\right)^2}\)
\(=\sqrt{\left(6m-18\right)^2+12^2}+\sqrt{\left(12-6m\right)^2+12^2}\)
\(=\sqrt{\left(18-6m\right)^2+12^2}+\sqrt{\left(6m-12\right)^2+12^2}\)
\(Q\ge\sqrt{\left(18-6m+6m-12\right)^2+\left(12+12\right)^2}=6\sqrt{17}\)
\(\Rightarrow a-b=-11\)

Gọi G là trọng tâm tam giác ABC
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1}{3};y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{1}{3}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất khi \(3MG\) nhỏ nhất
\(\Leftrightarrow M\) là hình chiếu của \(G\) trên trục tung
\(\Leftrightarrow M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\le3MG=1\)
Đẳng thức xảy ra khi \(M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\) Tung độ \(y_M=\dfrac{1}{3}\)

Gọi \(I\left(x_0;y_0\right)\) là điểm thỏa mãn \(\overrightarrow{IA}+\text{}\overrightarrow{IB}=\overrightarrow{0}\)
Ta có \(\left\{{}\begin{matrix}1-x_0+2-x_0=0\\3-y_0+7-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_0=3\\2y_0=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\frac{3}{2}\\y_0=5\end{matrix}\right.\)
\(\Rightarrow I\left(\frac{3}{2};5\right)\)
Khi đó \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}\right|=\left|2\overrightarrow{MI}+\overrightarrow{0}\right|=2MI\)
Lại có \(\left|\overrightarrow{MA}-\overrightarrow{MC}\right|=\left|\overrightarrow{CA}\right|=CA=\sqrt{\left(-1-2\right)^2+\left(3-7\right)^2}=5\)
Nên \(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|\overrightarrow{MA}-\overrightarrow{MC}\right|\)
\(\Leftrightarrow2MI=5\Rightarrow MI=\frac{5}{2}\)
Vậy \(M\in\left(I;\frac{5}{2}\right)\)

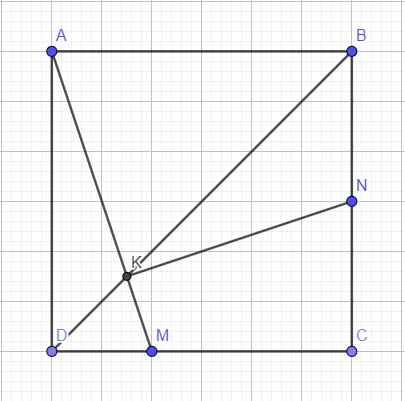
Talet: \(\dfrac{KM}{AK}=\dfrac{DM}{AB}=\dfrac{1}{3}\Rightarrow KM=\dfrac{1}{3}AK\Rightarrow KM=\dfrac{1}{4}AM\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AM}\)
Mà \(\overrightarrow{AM}=\overrightarrow{AD}+\overrightarrow{DM}=\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\Rightarrow\overrightarrow{KM}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}\)
\(\overrightarrow{KN}=\overrightarrow{KM}+\overrightarrow{MC}+\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{AD}+\dfrac{1}{12}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AB}-\dfrac{1}{2}\overrightarrow{AD}\)
\(=\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{KN}=\left(\overrightarrow{AD}+\dfrac{1}{3}\overrightarrow{AB}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)=\dfrac{1}{4}AB^2-\dfrac{1}{4}AD^2=0\)
\(\Rightarrow AM\perp KN\Rightarrow\) đường thẳng KN nhận (10;1) là 1 vtpt
Phương trình NK:
\(10\left(x-0\right)+1\left(y-2019\right)=0\Leftrightarrow10x+y-2019=0\)
\(d\left(O;NK\right)=\dfrac{\left|-2019\right|}{\sqrt{10^2+1^2}}=\dfrac{2019}{\sqrt{101}}\)

a.
Gọi G là trọng tâm tam giác ABC \(\Rightarrow\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Rightarrow T=\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(=\left|3\overrightarrow{MG}\right|=3\left|\overrightarrow{MG}\right|\)
\(\Rightarrow T_{min}\) khi và chỉ khi \(MG_{min}\Rightarrow MG=0\) hay M trùng G
Theo công thức trọng tâm: \(\left\{{}\begin{matrix}x_M=\dfrac{2-1+6}{3}=\dfrac{7}{3}\\y_M=\dfrac{3-1+0}{3}=\dfrac{2}{3}\end{matrix}\right.\) \(\Rightarrow M\left(\dfrac{7}{3};\dfrac{2}{3}\right)\)
b.
Tương tự câu a, ta có \(T=3\left|\overrightarrow{MG}\right|\) đạt min khi MG đạt min
\(\Rightarrow\) M là hình chiếu vuông góc của G lên Ox
Mà \(G\left(\dfrac{7}{3};\dfrac{2}{3}\right)\Rightarrow M\left(\dfrac{7}{3};0\right)\)
c.
Do M thuộc Ox nên tọa độ có dạng: \(M\left(m;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(2-m;3\right)\\\overrightarrow{MB}=\left(-1-m;-1\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{u}=\left(3m+6;7\right)\)
\(\Rightarrow\left|\overrightarrow{u}\right|=\sqrt{\left(3m+6\right)^2+7^2}\ge\sqrt{0+7^2}=7\)
Dấu "=" xảy ra khi \(3m+6=0\Rightarrow m=-2\)
\(\Rightarrow M\left(-2;0\right)\)

1.
Lấy điểm A' đối xứng với A qua Ox \(\Rightarrow A\left(-2;-1\right)\)
M có tọa độ \(M\left(x;0\right)\)
Ta có \(AM+MB=A'M+MB\ge AB=\sqrt{4^2+5^2}=\sqrt{41}\)
\(min=41\Leftrightarrow M,A',B\) thẳng hàng
\(\Leftrightarrow\overrightarrow{A'M}=k\overrightarrow{A'B}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2=k.4\\1=k.5\end{matrix}\right.\Rightarrow x=-\dfrac{6}{5}\Rightarrow M\left(-\dfrac{6}{5};0\right)\)
2.
Gọi N là trung điểm BC
\(\overrightarrow{MA}.\left(\overrightarrow{MB}+\overrightarrow{MC}\right)=0\)
\(\Leftrightarrow2\overrightarrow{MA}.\overrightarrow{MN}=0\)
\(\Leftrightarrow2MA.MN.cosAMN=0\)
\(\Leftrightarrow\left[{}\begin{matrix}MA=0\\MN=0\\cosAMN=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}M\equiv A\\M\equiv N\\\widehat{AMN}=90^o\end{matrix}\right.\)
\(\Rightarrow M\) thuộc đường tròn đường kính AN

\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
Gọi \(M\left(x;0\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-x;1\right)\\\overrightarrow{MB}=\left(1-x;3\right)\\\overrightarrow{MC}=\left(-2-x;2\right)\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\left(-2x+4;5\right)\)
\(\left|\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}\right|=\sqrt{\left(-2x+4\right)^2+5}\ge\sqrt{5}\)
Dấu "=" xảy ra khi \(-2x+4=0\Leftrightarrow x=2\Rightarrow M\left(2;0\right)\)