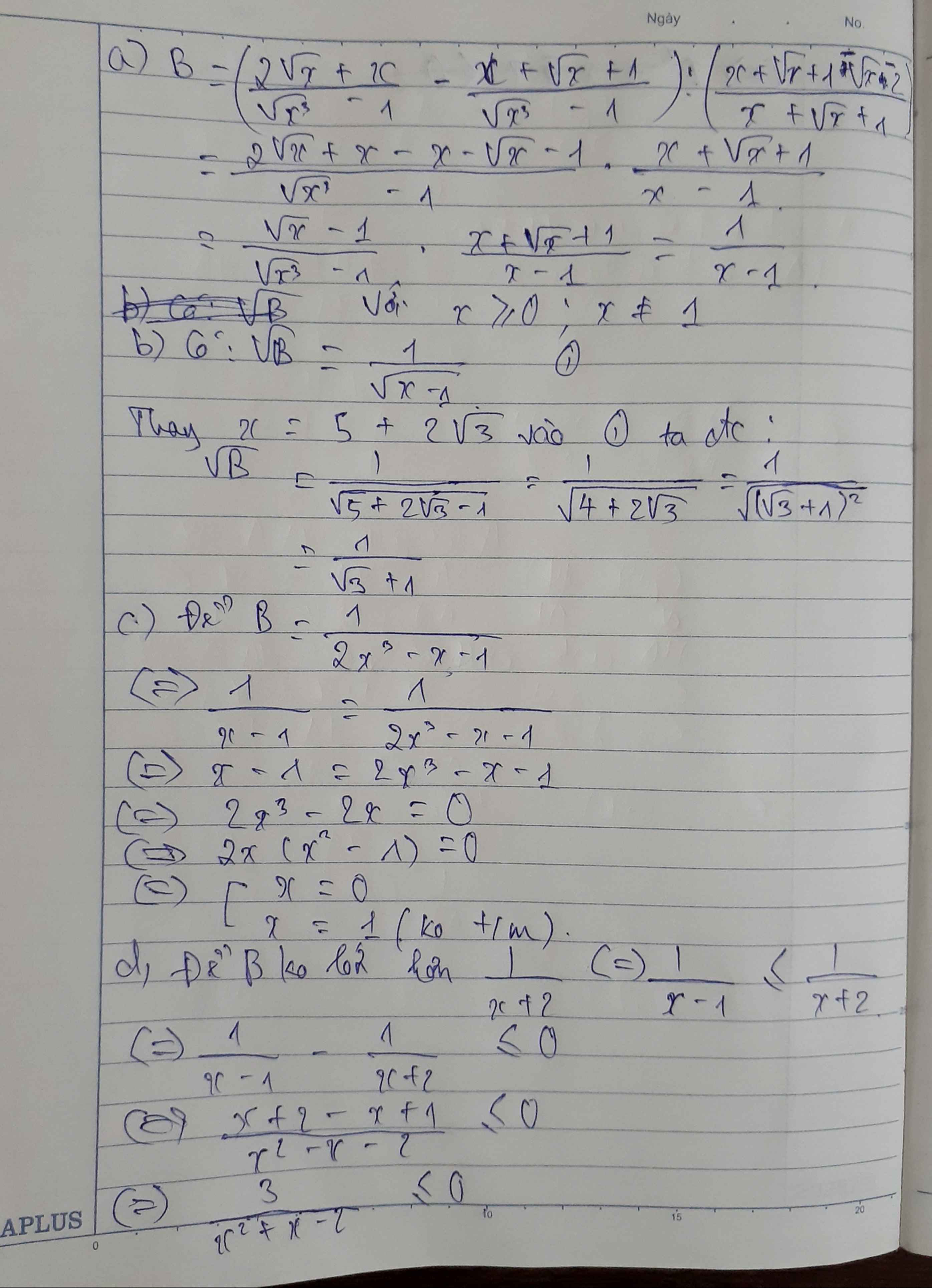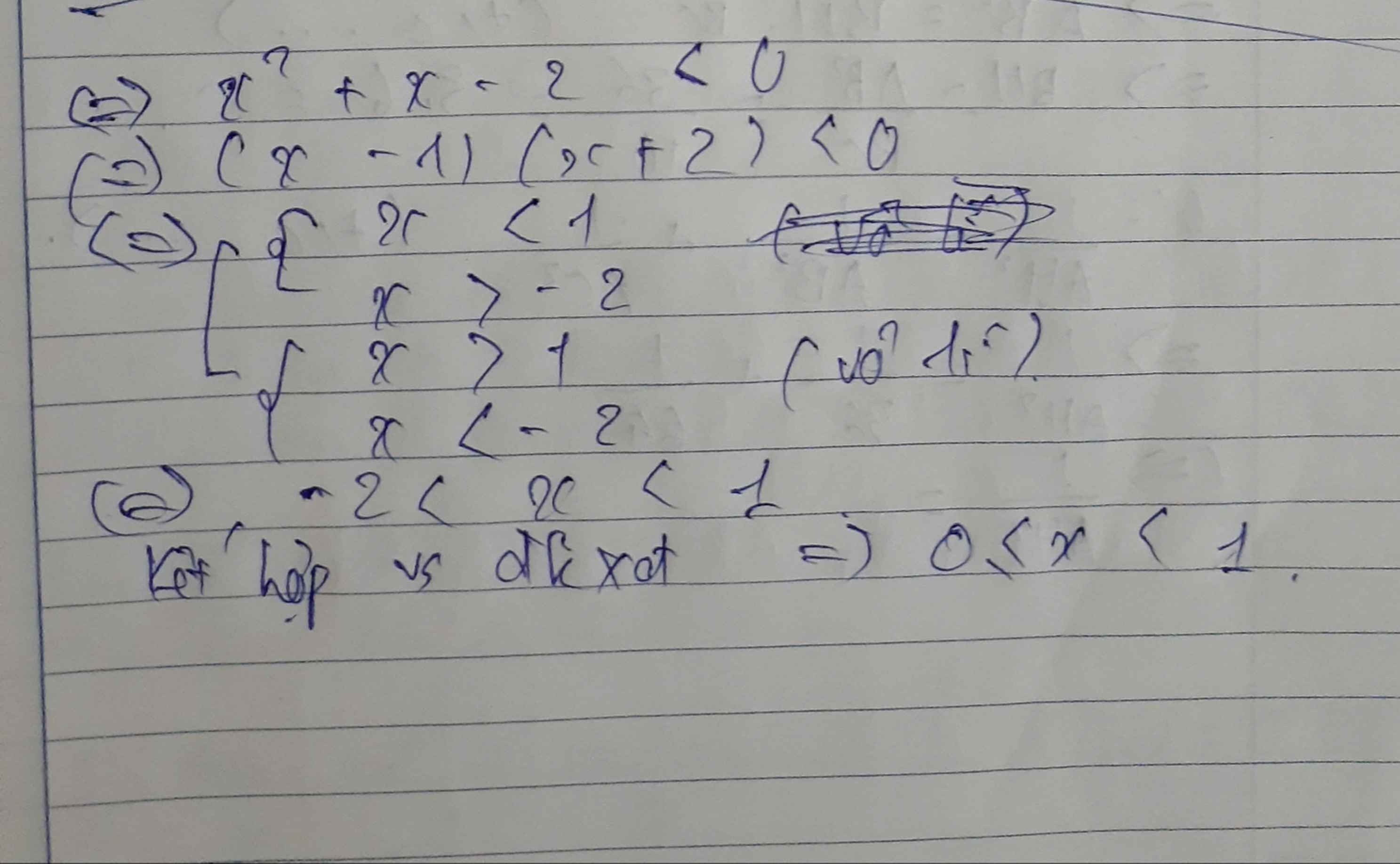Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\) Rút gọn
\(A=\dfrac{3}{\sqrt{7}-2}+\sqrt{\left(\sqrt{7}-3\right)^2}\)
\(=\dfrac{3}{\sqrt{7}-2}+\left|\sqrt{7}-3\right|\)
\(=\dfrac{3}{\sqrt{7}-2}+3-\sqrt{7}\)
\(=\dfrac{3+\left(3-\sqrt{7}\right)\left(\sqrt{7}-2\right)}{\sqrt{7}-2}\)
\(=\dfrac{3+3\sqrt{7}-6-7+2\sqrt{7}}{\sqrt{7}-2}\)
\(=\dfrac{5\sqrt{7}-10}{\sqrt{7}-2}\)
\(=\dfrac{5\left(\sqrt{7}-2\right)}{\sqrt{7}-2}\)
\(=5\)
Vậy \(A=5\)
\(B=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{x-1}\left(dkxd:x\ge0,x\ne1\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}\right).\left(\dfrac{x-1}{\sqrt{x}+1}\right)\)
\(=\dfrac{\sqrt{x}.\sqrt{x}-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}}{x-\sqrt{x}}.\left(\sqrt{x}-1\right)\)
\(=\sqrt{x}-1\)
Vậy \(B=\sqrt{x}-1\)
\(b,\) Để \(B< A\) thì \(\sqrt{x}-1< 5\)
\(\Leftrightarrow\sqrt{x}< 6\)
\(\Leftrightarrow x< 36\)

a) \(A=\sqrt{28}-\sqrt{63}+\dfrac{7+\sqrt{7}}{\sqrt{7}}-\sqrt{\left(\sqrt{7}+1\right)^2}\)
\(=2\sqrt{7}-3\sqrt{7}+\dfrac{\sqrt{7}\left(\sqrt{7}+1\right)}{\sqrt{7}}-\left|\sqrt{7}+1\right|\)
\(=-\sqrt{7}+\sqrt{7}+1-\sqrt{7}-1=-\sqrt{7}\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}-3}\right)\dfrac{4\sqrt{x}+12}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-3+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{4\left(\sqrt{x}+3\right)}{\sqrt{x}}\)
\(=\dfrac{8}{\sqrt{x}-3}\)
b) \(A>B\Rightarrow-\sqrt{7}>\dfrac{8}{\sqrt{x}-3}\Rightarrow\dfrac{8}{\sqrt{x}-3}+\sqrt{7}< 0\)
\(\Rightarrow\dfrac{\sqrt{7x}+8-3\sqrt{7}}{\sqrt{x}-3}< 0\)
Ta có: \(\left\{{}\begin{matrix}8=\sqrt{64}\\3\sqrt{7}=\sqrt{63}\end{matrix}\right.\Rightarrow8-3\sqrt{7}>0\Rightarrow8-3\sqrt{7}+\sqrt{7x}>0\)
\(\Rightarrow\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Rightarrow x< 9\Rightarrow0< x< 9\)

a) \(B=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\left(1-\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\right)\left(x\ge0,x\ne1\right)\)
\(=\left(\dfrac{2\sqrt{x}+x}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{x+\sqrt{x}+1-\sqrt{x}-2}{x+\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+x-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x-1}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{x+\sqrt{x}+1}{x-1}=\dfrac{1}{x-1}\)

\(a,A=\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\left(x>0;x\ne1\right)\\ A=\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\\ A=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(b,\dfrac{P}{A}\left(x-1\right)=0\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\cdot\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}+1\right)=0\\ \Leftrightarrow x=0\left(\sqrt{x}+1>0\right)\)
a) \(A=\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\left(đk:x>0,x\ne1\right)\)
\(=\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
b) \(\dfrac{P}{A}\left(x-1\right)=0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-1}:\dfrac{\sqrt{x}+1}{\sqrt{x}}.\left(x-1\right)=0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}+1\right)=0\)
\(\Leftrightarrow x=0\)( do \(\sqrt{x}+1\ge1>0\))(không thỏa đk)
Vậy \(S=\varnothing\)

a: \(=\dfrac{4x-8\sqrt{x}+8x}{x-4}:\dfrac{\sqrt{x}-1-2\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}\left(3\sqrt{x}-2\right)}{x-4}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{-\sqrt{x}+3}=\dfrac{-4x\left(3\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}\)
b: \(m\left(\sqrt{x}-3\right)\cdot B>x+1\)
=>\(-4xm\left(3\sqrt{x}-2\right)>\left(\sqrt{x}+2\right)\cdot\left(x+1\right)\)
=>\(-12m\cdot x\sqrt{x}+8xm>x\sqrt{x}+2x+\sqrt{x}+2\)
=>\(x\sqrt{x}\left(-12m-1\right)+x\left(8m-2\right)-\sqrt{x}-2>0\)
Để BPT luôn đúng thì m<-0,3

\(1,ĐKx\ge5\)
\(\sqrt{\left(x-5\right)\left(x+5\right)}+2\sqrt{x-5}=3\sqrt{x+5}+6\)
\(\Rightarrow\sqrt{x-5}\left(\sqrt{x+5}+2\right)-3\left(\sqrt{x+5}+2\right)=0\)
\(\Rightarrow\left(\sqrt{x+5}+2\right)\left(\sqrt{x-5}-3\right)=0\)
\(\left[{}\begin{matrix}\sqrt{x+5}=-2loại\\\sqrt{x-5}=3\end{matrix}\right.\)\(\Rightarrow x-5=9\Rightarrow x=14\)(TMĐK)
2a,ĐK \(x\ge0;x\ne9\)
,\(B=\dfrac{7\left(3-\sqrt{x}\right)-12}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}=\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}\)
\(M=\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(3-\sqrt{x}\right)}=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}+\dfrac{9-7\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
\(M=\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

Lời giải:
ĐKXĐ: $x>0; x\neq 4$
Sửa lại đề 1 chút.
\(A=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right).\frac{\sqrt{x}-2}{\sqrt{x}}=\frac{\sqrt{x}-2+\sqrt{x}+2}{(\sqrt{x}+2)(\sqrt{x}-2)}.\frac{\sqrt{x}-2}{\sqrt{x}}=\frac{2\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.\frac{\sqrt{x}-2}{\sqrt{x}}\)
\(=\frac{2}{\sqrt{x}+2}\)
\(B=\frac{7}{3}A=\frac{14}{3(\sqrt{x}+2)}\)
Với mọi $x>0$ thì hiển nhiên $B>0$. Mặt khác, $\sqrt{x}+2\geq 2$ nên $B=\frac{14}{3(\sqrt{x}+2)}\leq \frac{14}{6}=\frac{7}{3}$
Vậy $0< B\leq \frac{7}{3}$. $B$ đạt giá trị nguyên thì $B=1;2$
$B=1\Leftrightarrow \frac{14}{3(\sqrt{x}+2)}=1$
$\Leftrightarrow x=\frac{64}{9}$ (thỏa mãn)
$B=2\Leftrightarrow \frac{14}{3(\sqrt{x}+2)}=2$
$\Leftrightarrow x=\frac{1}{9}$ (thỏa mãn)

\(a,A=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{2}{2-\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right):\left(\sqrt{x}-2+\dfrac{10-x}{\sqrt{x}+2}\right)\left(dk:x\ge0,x\ne4\right)\\ =\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{2}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\left(\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)+10-x}{\sqrt{x}+2}\right)\\ =\dfrac{\sqrt{x}-2\left(\sqrt{x}+2\right)+\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}+2}{x-4+10-x}\)
\(=\dfrac{\sqrt{x}-2\sqrt{x}-4+\sqrt{x}-2}{\sqrt{x}-2}.\dfrac{1}{6}\\ =\dfrac{-6}{\left(\sqrt{x}-2\right).6}\\
=-\dfrac{1}{\sqrt{x}-2}\)
\(b,A>0\Leftrightarrow-\dfrac{1}{\sqrt{x}-2}>0\Leftrightarrow\sqrt{x}-2< 0\\
\Leftrightarrow\sqrt{x}< 2\Leftrightarrow x< 4\)
Kết hợp với \(dk:x\ge0,x\ne4\), ta kết luận \(0\le x< 4\)