Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

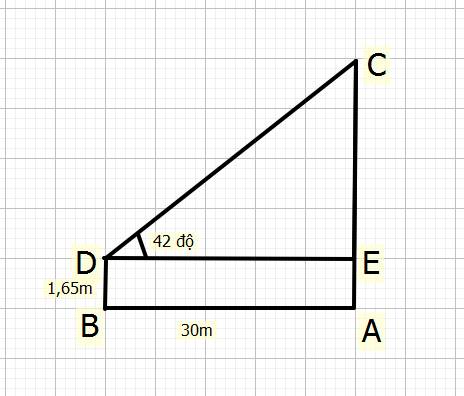
Xét \(\Delta ECD\) vuông tại `E`
Ta có:\(Tan\widehat{D}=\dfrac{EC}{ED}\left(tslg\right)\)
\(\Rightarrow Tan42^o=\dfrac{EC}{30}\\ \Rightarrow EC=30\cdot Tan30^o\\ \Rightarrow EC\approx27m\)
Chiều cao của ống khói đó là:
\(AC=EC+EA\\ \Rightarrow AC=27+1,65\approx28,65m\)
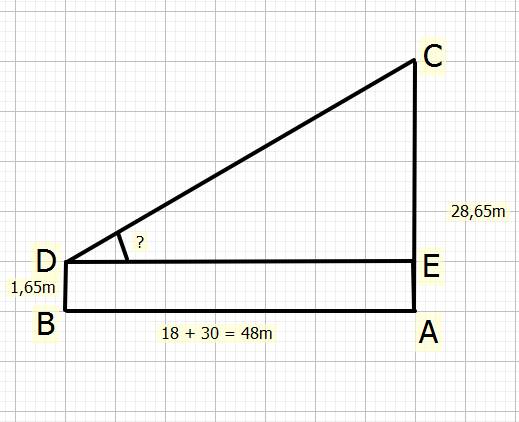
Xét \(\Delta CED\) vuông tại `E`
Ta có: \(Tan\widehat{D}=\dfrac{EC}{ED}\left(tslg\right)\)
\(\Rightarrow Tan\widehat{D}=\dfrac{28,65}{18+30}\\ \Rightarrow Tan\widehat{D}\approx30^o50'.\)

Diện tích bề mặt được sơn của phần thân ống khói:
\(S=2\pi rh=2\pi\left(\dfrac{0,3}{2}\right).15=0,45\pi\left(m\right)\approx1,414\left(m\right)\)

Gọi C là điểm đặt mắt người đó, BE là chiều cao của cây và CF là chiều cao người đó
Xét tứ giác AECF có:
\(\widehat{A}=\widehat{E}=\widehat{F}=90^0\)
=> AECF là hình chữ nhật
=> \(AE=CF=1,7m;AC=EF=30m\)
Áp dụng tslg trong tam giác ABC:
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=30.tan35^0\approx21\left(m\right)\)
Chiều cao của cây: \(BE=AB+AE\approx21+1,7\approx23\left(m\right)\)
Lời giải:
Theo hình vẽ ta có:
$BC=DE=1,7$ (m)
$AB=BE.\tan \widehat{AEB}=30.\tan 35^0=21$ (m)
Chiều cao của cây là:
$AC=AB+BC=21+1,7=22,7$ (m)

Với góc nhìn tạo với phương nằm ngang là 42 độ, ta có:
tan(42°) = h / 15
Để tìm giá trị của h, ta cần giải phương trình trên để tìm giá trị của h.
tan(42°) = h / 15
h = tan(42°) * 15
Sử dụng máy tính, ta tính được:
h ≈ 15.7m
Vậy, chiều cao của cây là khoảng 15.7m.