Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Bán kính trong khối bê tông: $r=1:2=0,5$ (m)
Bán kính ngoài khối bê tông: $R=0,5+0,01=0,51$ (m)
Thể tích khối bê tông cần sử dụng:
$\pi R^2h-\pi r^2h=\pi 0,51^2.1000-\pi 0,5^2.1000=10,1\pi$ (m3)

Thể tích hình trụ bên trong là:
pi*1^2*1,6=1,6pi(m3)
Bán kính hình trụ bên ngoài là:
1+0,1=1,1(m)
=>V hình trụ bên ngoài là: 1,1^2*1,6*pi=1,936*pi(m3)
Thể tích bể tông 1 ống là:
1,936pi-1,6pi=0,336pi(m3)
=>V bê tông 500 ống là: 500*0,336pi=527,52m3
Số bao xi măng cần tới là:
527,52*7=3692,64(bao)

Diện tích xung quanh của ống hình trụ :
S x q = 2πrb ( c m 2 )
Diện tích đáy của ống hình trụ :
S đ á y = π r 2 ( c m 2 )
Vì sơn cả bên ngoài lẫn bên trong ống nên diện tích ống được sơn bao phủ bằng hai lần diện tích xung quanh và hai lần diện tích đáy
S = 2.2 π rb + 2 π r 2 = 2( π r 2 + 2 π rb) ( c m 2 )
Vậy chọn đáp án A

Diện tích bề mặt được sơn của phần thân ống khói:
\(S=2\pi rh=2\pi\left(\dfrac{0,3}{2}\right).15=0,45\pi\left(m\right)\approx1,414\left(m\right)\)

Diện tích sơn cần dùng chính là diện tích xung quanh hình trụ
Diện tích đáy: \(S_đ=\pi R^2=\pi.\left(0,1\right)^2=\dfrac{\pi}{100}\left(m^2\right)\)
Diện tích xung quanh: \(S_{xq}=h.S_đ=\dfrac{4.\pi}{100}=\dfrac{\pi}{25}\left(m^2\right)\)

Thể tích của ống trụ là:

Chiều cao của hình trụ là h=20m.
Từ công thức V=Sh
![]()

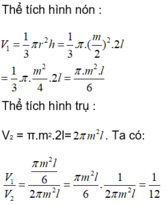
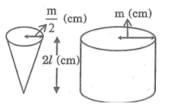
Vậy khi múc đầy nước vào hình nón và đổ vào hình trụ (Không chứa gì cả) thì độ cao của nước trong hình trụ là 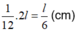
Vậy chọn đáp án A



V=200*pi*40^2=320000pi(cm3)