Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
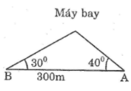
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
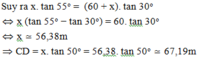
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
Gọi C là vị trí của máy bay.
Kẻ CH ⊥ AB
Trong tam giác vuông ACH, ta có:
AH = CH.cotgA (1)
Trong tam giác vuông BCH, ta có:
BH = CH.cotgB (2)
Từ (1) và (2) suy ra: (AH + BH) = CH.cotgA + CH.cotgB
Suy ra: CH =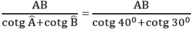 
≈ 102,606 (cm)
Gọi giao điểm của đường nhìn thấy máy bay tại A và B là C.
Vẽ CH vuông góc AB
=>CH là độ cao của máy bay
góc ACB=180-40-32=108 độ
Xét ΔACB có
AB/sin C=AC/sinB=BC/sin A
=>400/sin108=AC/sin32=BC/sin40
=>\(AC\simeq222,9\left(m\right);BC\simeq270,3\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinC=\dfrac{1}{2}\cdot222.9\cdot270.3\cdot sin108\simeq28650,52\left(m^2\right)\)
Độ cao là:"
28650,52*2/400\(\simeq143\left(m\right)\)
Gọi C là vị trí của máy bay
Gọi CH là độ cao của máy bay so với mặt đất
=>CH\(\perp\)AB tại H
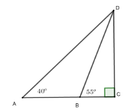
Ta có hình vẽ sau:
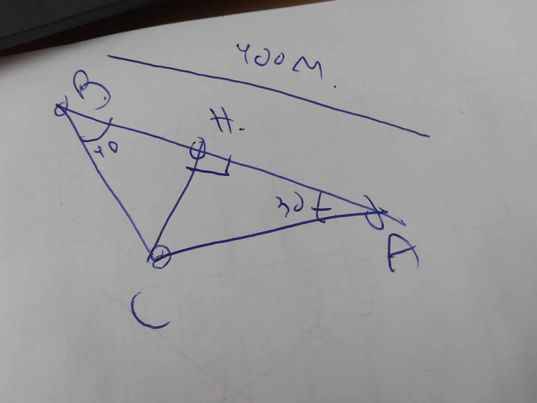
Xét ΔCBA có \(\widehat{CBA}+\widehat{CAB}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+30^0+40^0=180^0\)
=>\(\widehat{ACB}=110^0\)
Xét ΔABC có \(\dfrac{BA}{sinACB}=\dfrac{AC}{sinB}=\dfrac{BC}{sinA}\)
=>\(\dfrac{400}{sin110}=\dfrac{AC}{sin40}=\dfrac{BC}{sin30}\)
=>\(AC\simeq273,62\left(m\right);BC\simeq212,84\left(m\right)\)
Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot CA\cdot CB\cdot sinACB\)
\(=\dfrac{1}{2}\cdot273,62\cdot212,84\cdot sin110\simeq27362,57\left(m^2\right)\)
Xét ΔACB có CH là đường cao
nên \(\dfrac{1}{2}\cdot CH\cdot AB=S_{ABC}\)
=>\(CH\cdot\dfrac{400}{2}=27362,57\)
=>\(CH\simeq136,81\left(m\right)\)
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m