Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải:
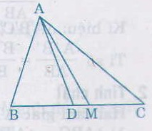
Ta có AD là đường phân giác của ∆ ABC nên
= = (kết quả ở bài 16)
=> =
hay = => = .
Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.
=> = -
=> = S -S =
a)
Có AB < AC (vì n > m) (1)
Ta có: \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\) ( vì AD là phân giác của góc BAC) (2)
Từ (1) và (2), ta có BD < CD
⇒ D nằm giữa B và M
Đặt S1, S2 lần lượt là diện tích △ADM và △ADC
Ta có: \(\dfrac{S_1}{S_2}=\dfrac{\dfrac{1}{2}.BD.AH}{\dfrac{1}{2}.CD.AH}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{m}{n}\)
⇒ \(\dfrac{S_1+S_2}{S_2}=\dfrac{m+n}{n}=\dfrac{S}{S_2}=\dfrac{m+n}{n}\Rightarrow S_2=\dfrac{n.S}{m+n}\)
Vì \(S_{AMC}=S_{AMB}=\dfrac{1}{2}.S\Rightarrow\)diện tích của △ADM là
\(S_{ADM}=S_{ADC}-S_{AMC}=S_2-\dfrac{1}{2}.S=\dfrac{n.S}{m+n}-\dfrac{1}{2}.S=\left[\dfrac{n-m}{2\left(m+n\right)}\right].S\)
b)
\(S_{ADM}=\left[\dfrac{7-3}{2\left(7+3\right)}\right].S=\dfrac{2}{10}.S=\dfrac{1}{5}.S=0,2.S=20\%.S\)
Vậy diện tích của △ADM bằng 20% diện tích của △ABC
a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)
Kẻ \(AH\perp BC\left(H\in BC\right)\)
Ta có: \(AB^2+AC^2=BC^2\left(3^2+4^2=5^2\right)\Rightarrow\Delta ABC\) vuông tại A
\(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH.5=3.4\Rightarrow AH=2,4\left(cm\right)\)
AD là tia p/g của \(\widehat{BAC}\left(D\in BC\right)\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{3}{3+4}\Rightarrow\frac{DB}{BC}=\frac{3}{7}\Rightarrow\frac{DB}{5}=\frac{3}{7}\Rightarrow DB=\frac{15}{7}\left(cm\right)\)
\(BM=\frac{1}{2}BC=\frac{1}{2}.5=\frac{5}{2}\left(cm\right)\)
Do đó: \(DM=BM-BD=\frac{5}{2}-\frac{15}{7}=\frac{5}{14}\left(cm\right)\)
Vậy \(S_{ADM}=\frac{1}{2}AH.DM=\frac{1}{2}.2,4.\frac{5}{14}=\frac{3}{7}\left(cm^2\right)\)
a) Ta có: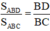
(do hai tam giác có chung chiều cao từ đỉnh A)
ΔABC có AD là phân giác
b) Với n = 7; m = 3, thay vào kết quả phần a ta có:
Vậy diện tích tam giác ADM chiếm 20% diện tích tam giác ABC.