Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1)
a) trong tam giac ABC vuong tai A co
+)BC2=AB2+AC2
suy ra AC=12cm
+)AH.BC=AB.AC
suy ra AH=7,2cm
b) Trong tu giac AMHN co HMA=HNA=BAC=90 do suy ra AMHN la hcn suy ra AH=MN=7,2cm
suy ra MN=7,2cm
c) goi O la giao diem cu MN va AH
Vi AMHN la hcn (cmt) nen OA=OH=7,2/2=3,6cm
suy ra SBMCN=1/2[OH*(MN+BC)]=39,96cm2
d) Vi AMHN la hcn nen goc AMN=goc HAB
Trong tam giac ABC vuong tai A co AK la dg trung tuyen ung voi canh huyen BC nen AK=BK=KC
suy ra tam giac AKB can tai K
suy ra goc B= goc BAK
Ta co goc B+ goc BAH=90 do
tuong duong BAK+AMN=90 do suy ra AK vuong goc voi MN (dmcm)

a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow AC^2=BC^2-AB^2=10^2-6^2=64\Rightarrow AC=8\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
tam giác AHB vuông tại H có đường cao HD nên áp dụng hệ thức lượng
\(\Rightarrow AD.AB=AH^2\)
tam giác AHC vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=AE.AC\Rightarrow AE.AC=AD.AB\Rightarrow\dfrac{AD}{AE}=\dfrac{AC}{AB}=\dfrac{8}{6}=\dfrac{4}{3}\)
b) Vì \(\angle ADH=\angle AEH=\angle DAE=90\Rightarrow ADHE\) là hình chữ nhật
\(\Rightarrow DE=AH\)
Ta có: \(BC.sinB.cosB=BC.\dfrac{AC}{BC}.\dfrac{AB}{BC}=\dfrac{AB.AC}{BC}=AH\)
\(\Rightarrow DE=BC.sinB.cosB\)

a: CH=6cm
\(AB=\sqrt{BH\cdot BC}=4\left(cm\right)\)
\(\widehat{C}=30^0\)

Lời giải:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$AH=2S_{ABC}:BC=AB.AC:BC=6.8:10=4,8$ (cm)
$\sin B = \frac{AC}{BC}=\frac{8}{10}=\frac{4}{5}$
b.
Áp dụng hệ thức lượng trong tam giác vuông ta có:
$BE.BA=BH^2$
$AF.AC=AH^2$
$\Rightarrow BE.BA+AF.AC=BH^2+AH^2=AB^2$ (đpcm)

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=81\Rightarrow AB=9\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.9}{15}=\dfrac{36}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=\dfrac{27}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=\dfrac{48}{5}\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại HA có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2=AE.AB\)
c) Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow AH=EF\)
tam giác EHF vuông tại H nên áp dụng Py-ta-go
\(\Rightarrow HE^2+HF^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HE^2+HF^2=HB.HC\)

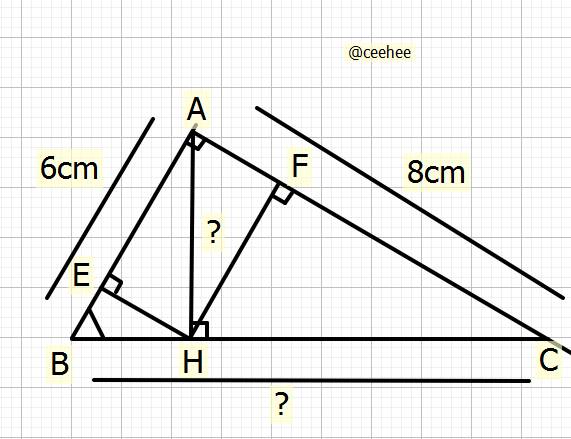
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)

Bài 1:
a: \(AC=\sqrt{10^2-6^2}=8\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=4.8\left(cm\right)\)
b: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)