Cho nửa đường tròn (O), đường kính AB, bán kính OC. Các điểm M, N thứ tự thuộc các cung AC, BC. Gọi E, G thứ tự là hình chiếu của M, N trên AB. Gọi F, H thứ tự là hình chiếu của M, N trên OC. Chứng minh rằng EF = GH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 3 2018
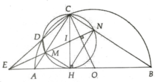
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm
30 tháng 3 2019
Câu 1 là vuông góc với AB chứ không phải vuông góc với A nha. Mình đánh nhanh nên nhầm
11 tháng 7 2021
a) Để DE lớn nhất thì AH lớn nhất
hay \(AH=\dfrac{BC}{2}\)
\(\Leftrightarrow\)ΔABC vuông cân tại A
hay điểm A là điểm chính giữa của (O)
