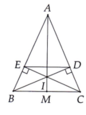
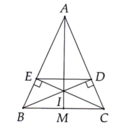
Cho tam giác ABC cân tại A (AB > BC). Vẽ BD AC tại D, CE
AC tại D, CE AB tại E.
AB tại E.
a) Chứng minh rằng :  và
và  ADE cân.
ADE cân.
b) Gọi H là giao điểm của BD và CE. Chứng minh rằng : AH là tia phân giác  .
.
c) Chứng minh rằng : AH > CH.
Các bạn giúp tớ nhé...