Cho hàm số y=-x^2 (P) và y=4x+4 (d) a) tìm toạ độ giao điểm của (P) và (d) b) xác định đường thẳng (d'): y=ax+b, biết d' song song d và d' cắt (P) tại điểm có hoành độ là -1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 10 2021
\(\left(d\right):y=ax+b//y=-\dfrac{1}{2}x+3\Leftrightarrow a=-\dfrac{1}{2}\left(1\right)\)
(d) cắt trục hoành tai điểm có hoành độ 2
\(\Leftrightarrow y=0;x=2\Leftrightarrow2a+b=0\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{1}{2}\\b=1\end{matrix}\right.\)
Vậy đths là \(y=-\dfrac{1}{2}x+1\)
19 tháng 10 2021
Vì (d)//y=-1/2x+3 nên \(a=-\dfrac{1}{2}\)
Thay x=2 và y=0 vào (d), ta được:
\(b+\dfrac{-1}{2}\cdot2=0\)
hay b=1
5 tháng 12 2023
Bài 1:
a: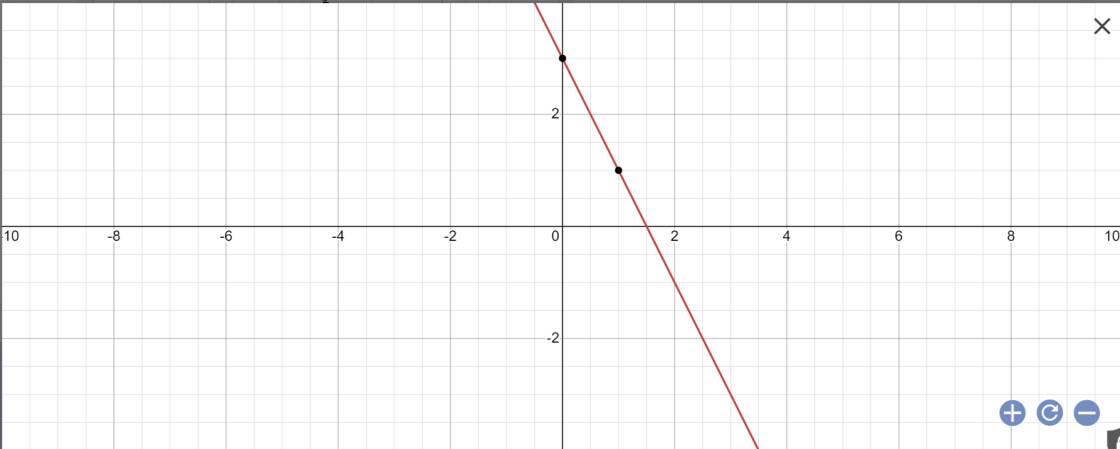 
b: Vì (d')//(d) nên \(\left\{{}\begin{matrix}a=-2\\b< >3\end{matrix}\right.\)
vậy: (d'): y=-2x+b
Thay x=2 và y=0 vào (d'), ta được:
\(b-2\cdot2=0\)
=>b-4=0
=>b=4
Vậy: (d'): y=-2x+4
18 tháng 11 2021
\(a,\Leftrightarrow\left\{{}\begin{matrix}a=3;b\ne1\\2a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-1\end{matrix}\right.\\ b,\Leftrightarrow\left\{{}\begin{matrix}a=1;b\ne-5\\B\left(-2;0\right)\inđths\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1;b\ne-5\\-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
a) pt hoành độ giao điểm \(x^2+4x+4=0\Rightarrow\left(x+2\right)^2=0\Rightarrow x=-2\)
\(\Rightarrow y=-\left(-2\right)^2=-4\Rightarrow\) tọa độ giao điểm là \(\left(-2;-4\right)\)
b) Vì \((d)\parallel (d')\Rightarrow \) \(\left\{{}\begin{matrix}a=4\\b\ne4\end{matrix}\right.\Rightarrow y=4x+b\)
Vì (d') cắt (P) tại điểm có hoành độ là -1 \(y=-\left(-1\right)^2=-1\)
\(\Rightarrow\) điểm đó có tọa độ là \(\left(-1;-1\right)\)
\(\Rightarrow-1=-4+b\Rightarrow b=3\Rightarrow y=4x+3\)