Cho ∆ABC vuông tại A có AC = 15cm, BC = 25cm. Tính diện tích hình tròn nt ∆ ABC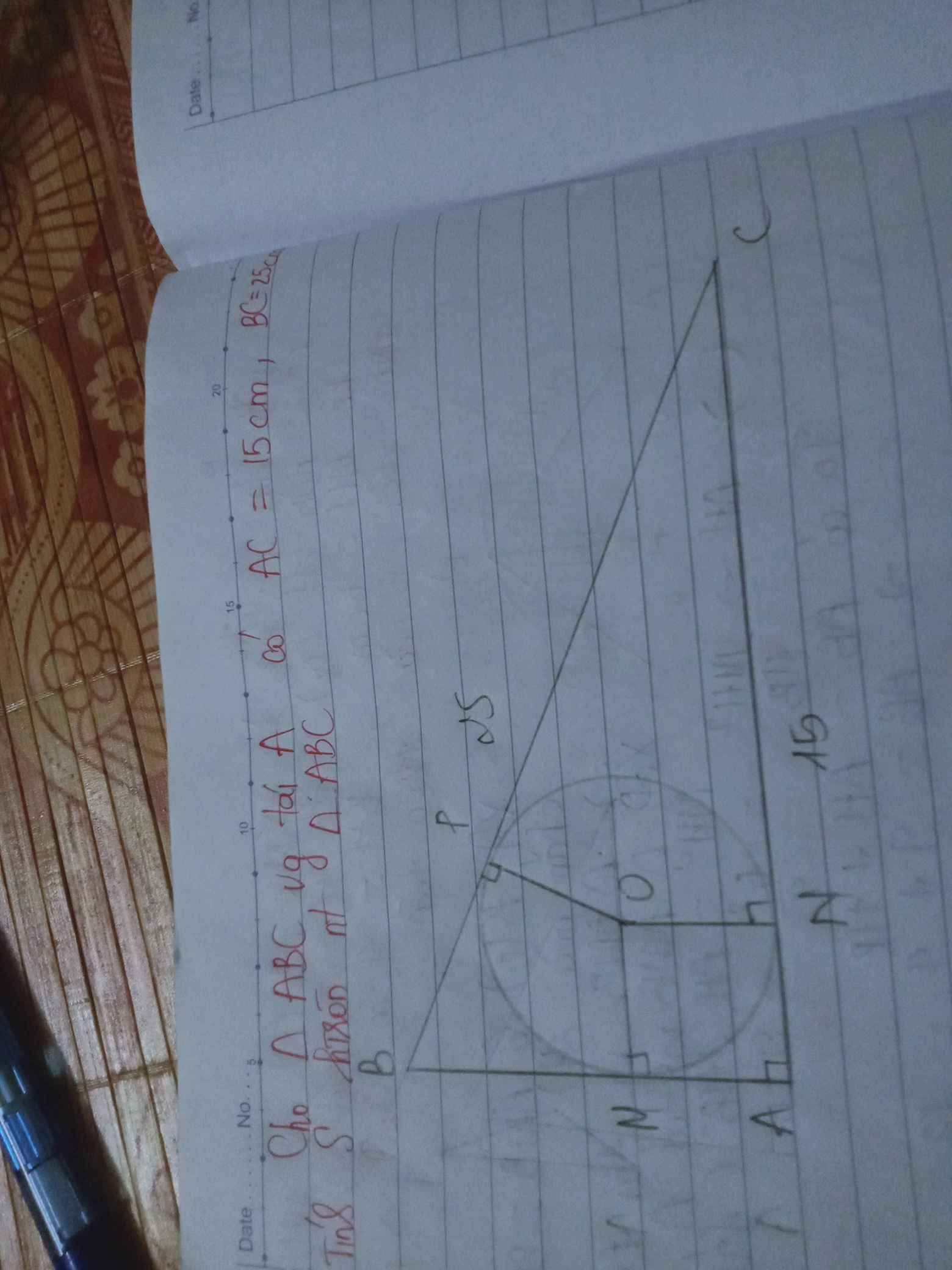
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
N
2
Những câu hỏi liên quan
12 tháng 1 2022
1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành
H9
HT.Phong (9A5)
CTVHS
28 tháng 9 2023
Xét tam giác ABC vuông tại A áp dụng Py-ta-go ta có:
\(AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-15^2}=20\left(cm\right)\)
Mà: \(sinB=\dfrac{AC}{BC}=\dfrac{15}{25}=\dfrac{3}{5}\)
\(\Rightarrow\widehat{B}\approx36^o52'\)
\(\Rightarrow\widehat{C}=180^o-90^o-36^o52'\approx53^o7'\)
19 tháng 9 2021
\(1,\)
\(a,\) Áp dụng HTL tam giác
\(\left\{{}\begin{matrix}AH^2=CH\cdot BH\\AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AH^2}{CH}=\dfrac{25}{6}\left(cm\right)\\AB=\sqrt{\dfrac{25}{6}\left(\dfrac{25}{6}+6\right)}=\dfrac{5\sqrt{61}}{6}\left(cm\right)\\AC=\sqrt{6\left(\dfrac{25}{6}+6\right)}=\sqrt{61}\left(cm\right)\end{matrix}\right.\\ BC=\dfrac{25}{6}+6=\dfrac{61}{6}\left(cm\right)\)
\(b,S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot5\cdot\dfrac{61}{6}=\dfrac{305}{12}\left(cm^2\right)\)
MK
23 tháng 2 2022
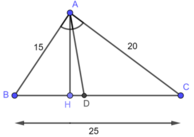
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)
như hình vẽ trên
xét tam giác ABC vuông tại A
=>\(AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-15^2}=20cm\)
nửa chu vi tam giác ABC : \(p=\dfrac{AB+AC+BC}{2}=\dfrac{15+25+20}{2}=30cm\)
diện tích tam giác ABC : \(S=\dfrac{AB.AC}{2}=\dfrac{20.15}{2}=150cm^2\)
bán kính đường tròn nội tiếp: \(R=\dfrac{S}{p}=\dfrac{150}{30}=5cm\)
=> diện tích hình tròn nt tam giác ABC:
\(S1=\pi,R^2=3,14.5^2=78,5cm^2\)