tìm x, biết
x4+4x3-4x2-48x-48=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 10 2021
b: \(8x^2-48x+6xy-36y\)
\(=8x\left(x-6\right)+6y\left(x-6\right)\)
\(=2\left(x-6\right)\left(4x+3y\right)\)
d: \(a^2-2ab+b^2-4\)
\(=\left(a-b\right)^2-4\)
\(=\left(a-b-2\right)\left(a-b+2\right)\)
16 tháng 2 2022
\(\Leftrightarrow4x^2\left(x-1\right)-\left(x-1\right)=0\Leftrightarrow\left(2x-1\right)\left(2x+1\right)\left(x-1\right)=0\Leftrightarrow x=\dfrac{1}{2};x=-\dfrac{1}{2};x=1\)
TD
16 tháng 2 2022
\(4x^3-4x^2-x+1=0\)
<=>\(\left(2x+1\right)\left(x-1\right)\left(2x-1\right)=0\)
<=>\(\left[{}\begin{matrix}x=\dfrac{-1}{2}\\x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
CM
12 tháng 12 2017
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: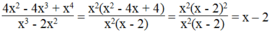 
Nếu phân thức có giá trị bằng 0 thì biểu thức x - 2 cũng có giá trị bằng 0. Suy ra: x - 2 = 0 ⇒ x = 2 mà x = 2 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức có giá trị bằng 0.
TC
Thầy Cao Đô
Giáo viên
VIP
19 tháng 12 2022
$4x^3 + x = 4x^2$
$\Leftrightarrow x(4x^2 - 4x + 1) = 0$
$\Leftrightarrow x(2x - 1)^2 = 0$
$\Leftrightarrow \left[\begin{aligned}&x = 0\\ &2x - 1 = 0\\ \end{aligned}\right. \Leftrightarrow \left[\begin{aligned}&x = 0\\ &x = \dfrac12\\ \end{aligned}\right.$
CM
16 tháng 3 2019
y ' = 12 x - 1 x 2 - 4 y ' = 0 ⇔ x = 1 ; x = ± 2
Lập bảng biến thiên và suy ra hàm số đạt cực đại tại điểm x 0 = 1
Đáp án A
CM
10 tháng 2 2019
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: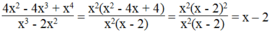 
Nếu phân thức đã cho bằng 2 thì biểu thức x - 2 cũng có giá trị bằng 2. Suy ra: x- 2 = 2 ⇒ x = 4. Với x = 4 thỏa mãn điều kiện.
Vậy khi x = 4 thì phân thức có giá trị bằng 2.
PT
1
CM
3 tháng 9 2018
Điều kiện: x 3 - 2 x 2 = x 2 x - 2 ≠ 0 ⇒ x ≠ 0 và x ≠ 2
Ta có: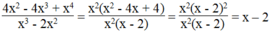 
Nếu phân thức đã cho bằng -2 thì biểu thức x - 2 cũng có giá trị bằng -2. Suy ra: x - 2 = -2 ⇒ x = 0 không thỏa mãn điều kiện.
Vậy không có giá trị nào của x để phân thức bằng -2
TN
1
CM
7 tháng 8 2018
Ta có y’=12x2+2mx-3.
Do ∆ ' = m 2 + 36 > 0 , ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị x1; x2.
Theo Viet, ta có x 1 + x 2 = - m 6 x 1 x 2 = - 1 4
Mà x1+4x2=0 suy ra
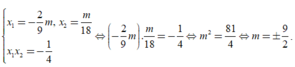
Chọn A.
x4+4x3-4x2-48x-48=0
=> x4+4(x3-x2) - 48x = 48
=> x4 + 4[x2(x-1)] - 48x = 48
\(x^4+4x^3-4x^2-48x-48=0\)
\(\Leftrightarrow\)\(x^4-2x^3-4x^2+6x^3-12x^2-24x+12x^2-24x-48=0\)
\(\Leftrightarrow\)\(x^2\left(x^2-2x-4\right)+6x\left(x^2-2x-4\right)+12\left(x^2-2x-4\right)=0\)
\(\Leftrightarrow\)\(\left(x^2-2x-4\right)\left(x^2+6x+12\right)\)
\(\Leftrightarrow\)\(\left[\left(x-1\right)^2-5\right]\left(x^2+6x+12\right)=0\)
\(\Leftrightarrow\)\(\left(x-1-\sqrt{5}\right)\left(x-1+\sqrt{5}\right)\left(x^2+6x+12\right)=0\)
Ta có: \(x^2+6x+12=\left(x+3\right)^2+3>0\)
\(\Rightarrow\)\(\orbr{\begin{cases}x-1-\sqrt{5}=0\\x-1+\sqrt{5}=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1+\sqrt{5}\\x=1-\sqrt{5}\end{cases}}\)
Vậy...