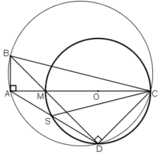
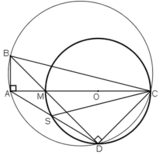
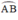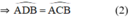Cho tam giác ABC vuông ở A, M là một điểm trên AC. Đường tròn đường kính CM cắt BM và BC lần lượt tại D và N, AD cắt đường tròn trên tại S.CMR
1) Bốn điểm A,B,C,D cùng thuộc một đường tròn
2) CA là tia phân giác của góc SCB
3) Các đường thẳng AB, NM , CD đồng quy.

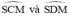 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 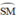
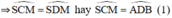
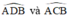 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung 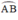
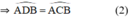

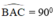 ⇒ A ∈ đường tròn đường kính BC.
⇒ A ∈ đường tròn đường kính BC.
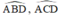 đều là góc nội tiếp chắn cung
đều là góc nội tiếp chắn cung 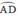
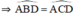
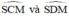 đều là các góc nội tiếp cùng chắn cung
đều là các góc nội tiếp cùng chắn cung 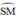
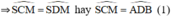
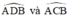 đều là các góc nội tiếp chắn cung
đều là các góc nội tiếp chắn cung