22a+33b=110115. tìm số tự nhiên a; b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
2
IW
13 tháng 7 2016
Ta có: 33.a+22.b=110115
=> 3a+2b=10010,45454545455
VÌ 33 và 22 đều chia hết cho 11 => 33.a+22.b đều chia hết cho 11
Tuy nhiên 110115 không chia hết cho 11 ( Vô lý)
=> a,b không tồn tại để 33.a+22.b= 110115
13 tháng 7 2016
33a + 22b = 11(3a+2b) chia hết cho 11 mà 110115 không chia hết cho 11 nên không tồn tại hai số tự nhiên a và b nào thỏa mãn đề bài.
TN
0
PT
1
11 tháng 4 2023
Hệ số tự do của đa thức chính là đơn thức có bậc bằng 0
`->` Hệ số tự do của đa thức trên là `-22`
`-> B.`
18 tháng 7 2016
33a+22b=110115
TH1:
33a=110115
a=110115:33
a=36705/11
=>22b=110115-(33.36705/11)
=>22b=0
b=0:22
=>b=0
TH2
33a+22b=110115
22b=110115
b=110115:22
b=110115/22
=>33a=110115-(22.110115/22)
33a=0
a=0:33
=> a=0
1 tháng 10 2015
a, 2a=b ta thay vào đẳng thức: 22a +b= 22a + 2a= 24 a= > a=2
ta có : 2a= b=> b=4
vậy a=2;b=4
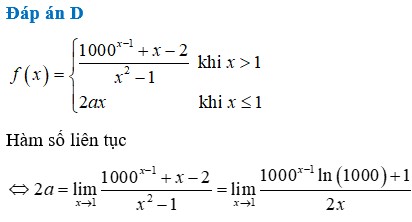
bn tham khảo trong câu hỏi tương tự á, có đó
33A+22B = 11(3A+2B) = 110115
-> 3A+2B = 110115 : 11 không là một số tự nhiên
Vậy không tìm được A,B thõa mãn yêu cầu đề bài