Cho tập XX có 2021 phần tử phân biệt, số các hoán vị của tập XX là
A.
4042
B.
2021!
22021
D.
20212
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để x < 0
=> a - 20 < 0
=> a < 20 (1)
mà a \(\inℕ^∗\)(2)
Từ (1) và (2) => \(a\in\left\{1;2;3;...;19\right\}\)
=> Số phần tử của tập S là : (19 - 1) : 1 + 1 = 19 phần tử

Đáp án cần chọn là: C
Các số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Vì vậy số phần tử của tập hợp A là:
2021–1980+1=42.

Đáp án B.
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x - m 2 x = x 2 - ( m - 1 ) x - m
⇔ x - m 2 x = ( x - m ) ( x + 1 ) ⇔ x - m 2 x - x - 1 = 0 ⇔ x = m 2 x = x + 1
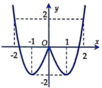
Giải phương trình 2 x = x + 1 .
![]()
Nhìn vào màn hình ta thấy phương trình 2 x = x + 1 có hai nghiệm phân biệt là x = 0 ; x = 1 . Do vậy để tập nghiệm của phương trình đã cho có đúng hai phần tử thì m ∈ 0 ; 1 . Vậy có 2 giá trị của m thỏa mãn, ta chọn B.

Đáp án D
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x . 2 x = x 2 - m x + x + m . 2 x - m
⇔ 2 x x - m = x + 1 x - m ⇔ 2 x - x - 1 x - m = 0 ⇔ [ 2 x - x - 1 = 0 ( 1 ) x - m = 0 ( 2 )
Giải (1) , đặt f x = 2 x - x - 1 . Xét hàm số f x = 2 x - x - 1 trên ℝ , có f ' x = 2 x . ln 2 - 1
Phương trình f ' x = 0 ⇔ 2 x = 1 ln 2 ⇔ x = log 2 1 ln 2 = - log 2 ln 2
⇒ f x = 0 có nhiều nhất 2 nghiệm mà f 0 = f 1 ⇒ f x = 0 ⇔ [ x = 0 x = 1
Để phương trình đã cho có hai nghiệm phân biệt ⇔ 2 có 1 nghiệm hoặc 0
Vậy m = {0;1} là hai giá trị cần tìm.
B
B