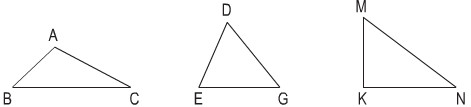
Bài 1. Viết tên ba góc và ba cạnh của mỗi hình tam giác dưới đây:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
30 tháng 8 2018
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
PT
1
CM
31 tháng 10 2019
- Hình tam giác ABC có ba góc là góc A, góc B, góc C và ba cạnh là AB, BC và CA.
- Hình tam giác DEG có ba góc là góc D, góc E, góc G và ba cạnh là DE, EG và GD.
- Hình tam giác KMN có ba góc là góc K, góc M, góc N và ba cạnh là KM, MN và NK.
MT
1 tháng 4 2017
Theo định nghĩa ta thấy kết quả:
a) HÌnh trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.
b) Hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, cond bán kính đáy bằng một nửađộ dài cạnh đáy của tam giác cân đó.
c) Khối nón tròn xoay.
d) Khối trụ tròn xoay.
26 tháng 8 2021
Bài 40:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: AD=DE
mà DE<DC
nên AD<DC
d: Ta có: ΔADF=ΔEDC
nên AF=EC
Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
Do đó: AE//CF
Hình 1. Ba góc là góc A, góc B, góc C
Ba cạnh là AB, AC, BC
Hình 2. Ba góc là : góc D, góc E, góc G
Ba cạnh là: DE, DG, EG
Hình 3. Ba góc là: góc M, góc K, góc N
Ba cạnh là MK, MN, KN.
chúc bạn hok tốt nhé!!