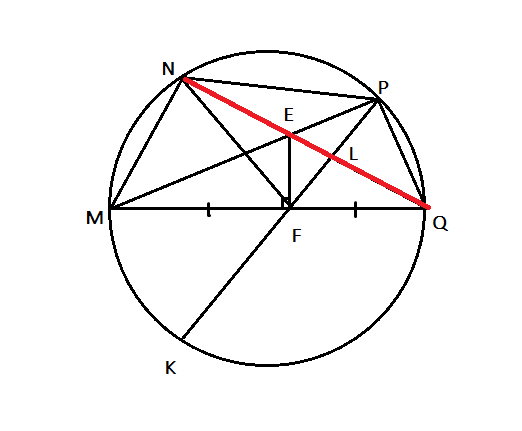
Cho hình vuông MNPQ, điểm A tùy ý trên đường chéo NQ, kẻ AE vuông góc với MN( E thuộc MN), AF vuông góc với MQ( F thuộc MQ). Hỏi:
a. Tứ giác MEAF là hình gì? Vì sao?
b. C/m QE=PF và QE vuông góc với PF
c. Xác định vị trí điểm A trên NQ để diện tích tứ giác MEAF lớn nhất. Tìm diện tích đó

MEAF là HCN vì M1=F1=E1=90 độ
b.QMN cân tại M ( -> Góc FQA=Góc N1)
Có QFA=AEN=90 ĐỘ
-> T/G QFA đồng dạng vs NEA -> A3=N1=FQA-> T/G QFA vuông cân tại F -> FQ=FA=ME
-Xét 2 tam giác PQF=QME(C.G.C)
-> QE=PF( 2 cạnh tương ứng ) -> P1=Q1 ( góc tương ưng )
có F3+P1=90 ĐỘ ( tam giác vuông ) mà P1=Q1 -> F3+Q1=90 ĐỘ -> QE vuông góc vs PF
c.Có FA+AE=ME+EN=MN( không đổi =>FA.AE lớn nhất khi FA=AE => MEAF là hình vuông khi A trùng vs giao điểm 2 đường chéo của hình vuông MNPQ
Diện tích hình vuông MEAF là FA.AE