Cho tam giác ABC cân tại A có góc B = góc C = 40 độ. Trên AB kéo dài về phía B lấy điểm M sao cho AM = BC.
Tính góc AMC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra, ta có \(\widehat{B}=\widehat{C}=40^o\)
\(\Rightarrow\widehat{A}=100^o\)
\(\Rightarrow\widehat{CBM}=100+40=180^o\)(TC góc ngoài tam giác)
Lại có \(BC=BM\Rightarrow\)Tam giác BMC cân tại B
\(\Rightarrow\widehat{BMC}=\widehat{BCM}=\left(180-140\right):2=20^o\)
Vậy AMC = 20 độ
À, nhầm chỗ góc CBM là 140 độ bạn nhé, không phải 180 độ đâu, mình đánh nhầm, còn lại phía dưới vẫn đúng bạn nhé

Trên nửa mặt phẳng bờ là AM có chứa điểm C dựng tam giác đều AMD, nối DC
Xét \(\Delta\)ABC cân tại A có ^ABC=^ACB=400 => ^BAC=1000
Do \(\Delta\)AMD đều => ^MAD=600 => ^CAD=^BAC - ^MAD = 400 => ^CAD=^ABC (=400) .
Ta có: AD=AM. Mà AM=BC => AD=BC
Xét \(\Delta\)ABC và \(\Delta\)CAD: AB=CA; ^ABC=^CAD (cmt); BC=AD (cmt)
=> \(\Delta\)ABC=\(\Delta\)CAD (c.g.c) => AC=CD => C thuộc trung trực của AD
Mà M cũng thuộc trung trực AD (Do MA=MD) => MC là trung trực của AD
Xét \(\Delta\)MAD đều có MC là trung trực cạnh AD => MC là phân giác ^AMD
=> ^AMC= 1/2.^AMD= 1/2. 600 = 300.
Vậy .....

hình bạn tự vẽ nhé
dựng tam giác AMN đều , nối M với C , N với C
Xét tam giác ABC và tam giác CAN có
AM=AN=BC
AC chung
góc CAN=góc ACB=40 độ
\(\Rightarrow\)tam giác ABC=tam giác CAN ( c.g.c)
\(\Rightarrow\)CN=AB=AC
Xét tam giác CMN và tam giác CMA có
AM=MN
AC=NC
CM chung
\(\Rightarrow\)tam giác CMN = tam giác CMA ( c.c.c)
\(\Rightarrow\)góc AMC=góc NMC=\(\frac{1}{2}\)góc AMN=30 độ

Tham khảo
Cho tam giác ABC cân tại A , góc A=20 độ , vẽ tam giác đều DBC , D nằm trong tam giác ABC . Tia phân giác của góc ABD cắt AC tại H . Chứng minh :
a) Tia AD là tia phân giác của góc BAC
b) AM = BC
Hình thì chắc bạn vẽ được nên tớ không vẽ nữa!!!![]()
![]()
![]()
a, Đi chứng minh tam giác ABD=tam giác ACD (c.c.c) =>góc BAD=góc CAD=>AD là tia phân giác của góc BAC(đpcm)
nếu có j thắc mắc hỏi mình nha!!!![]()
![]()
b, tớ sửa đề chứng minh AH=BC do không có điểm M.
Chứng minh
Xét tam giác ABC cân tại A ta có:
góc ABC=góc ACB=(180độ -20 độ):2=160 độ:2=80độ (theo tính chất của tam giác cân)
ta lại có: góc DBC=60 độ( theo tính chất của tam giác đều)
mà góc ABD=góc ABC-góc DBC=80độ -60 độ=20độ
mặt khác góc BAD=gócCAD=20độ/2=10độ và góc ABD=20độ/2=10độ (theo tính chất của tia phân giác)
Xét tam giác ABH và tam giác BAD ta có:
góc BAH=góc ABD (=20độ); AB: cạnh chung; góc ABH=góc BAD(=10độ)
Do đó tam giác ABH = tam giác BAD
=> AH=BD mà BD=BC( theo tính chất của tam giác đều) nên AH=BC (đpcm)
Có chỗ nào vướng mắc hỏi mình nha!! Chúc bạn học giỏi!!![]()
![]()

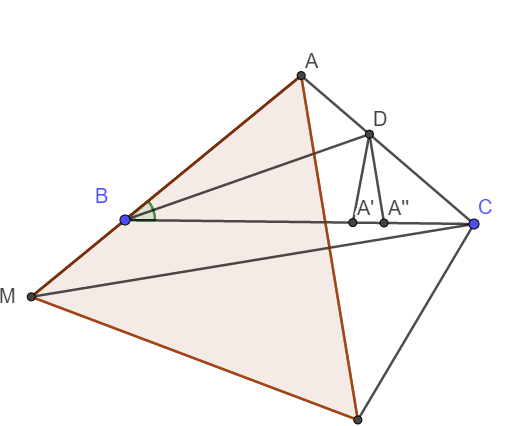
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA; BA'' = BD
Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\)
\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)
\(\Rightarrow\widehat{DA'A''}=80^o\)
Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)
Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)
Nên DA'' = CA''
Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD
b) Vẽ tam giác đều AMF.
Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)
Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)
\(\Rightarrow AC=CF\)
Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.
Vậy nên \(\widehat{MAC}=30^o\)
giúp mk, mk cho 2 k nha
30 độ nha