Cho Tam Giác ABC vuông Tại A Cod Góc ABC=60 Độ. Gọi M Là trung Điểm AC
Trên tia Đối Của Tia MB Lấy điểm D Sao cho MB=MD
a) Tính số đo góc ACB
b) Chứng minh tam giác ABM= Tam giác CDM
c) chứng mknh CD vuông góc AC
d) Chứng minh góc ABC= Góc CDA
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
25 tháng 11 2023
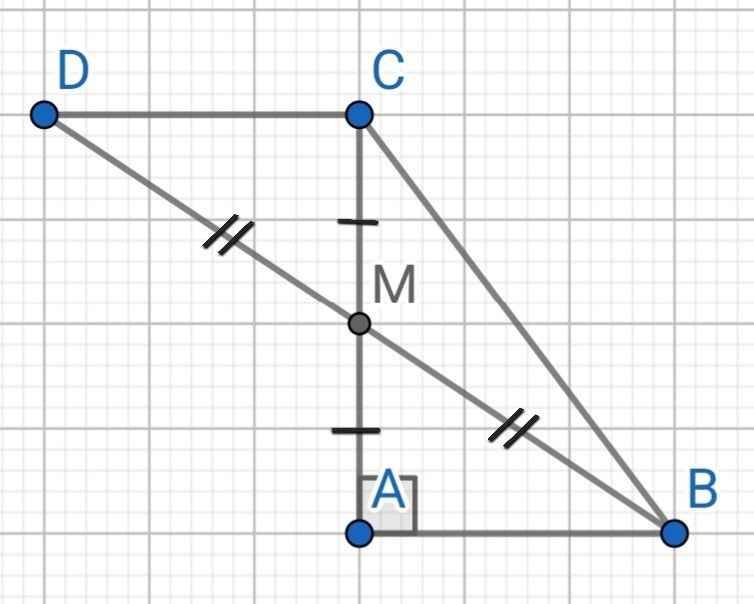a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD
3 tháng 12 2023
a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: ΔABM=ΔCDM
=>\(\widehat{MAB}=\widehat{MCD}=90^0\)
=>DC\(\perp\)AC
mà AC\(\perp\)AB
nên AB//DC
c: ΔMAB=ΔMCD
=>AB=CD
Xét ΔKAB và ΔKEC có
KA=KE
\(\widehat{AKB}=\widehat{EKC}\)
KB=KC
Do đó: ΔKAB=ΔKEC
=>AB=EC
ΔKAB=ΔKEC
=>\(\widehat{KAB}=\widehat{KEC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//EC
AB//EC
AB//CD
CD,EC có điểm chung là C
Do đó: E,C,D thẳng hàng
AB=EC
AB=CD
Do đó: EC=CD
Ta có: E,C,D thẳng hàng
EC=CD
Do đó: C là trung điểm của ED
17 tháng 12 2022
a: Xét ΔABM và ΔCDM có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔABM=ΔCDM
b: ΔABM=ΔCDM
nên AB=CD và góc ABM=góc CDM
=>AB//CD
=>CE vuông góc với AC
=>AC vuông góc DE
HH
16 tháng 12 2017
(Bạn tự vẽ hình giùm)
a/ \(\Delta ADM\)và \(\Delta CBM\)có: AM = CM (M là trung điểm của AC)
\(\widehat{AMD}=\widehat{BMC}\)(đối đỉnh)
DM = BM (gt)
=> \(\Delta ADM\)= \(\Delta CBM\)(c. g. c) => AD = BC (hai cạnh tương ứng)
b/ \(\Delta ABM\)và \(\Delta CDM\)có: AM = CM (M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(đối đỉnh)
BM = DM (gt)
=> \(\Delta ABM\)= \(\Delta CDM\)(c. g. c)
=> \(\widehat{BAM}=\widehat{MCD}=90^o\)(hai góc tương ứng)
=> AC _|_ CD (đpcm)
10 tháng 9 2021
a: Xét ΔABM và ΔCDM có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔABM=ΔCDM
b: Ta có: ΔABM=ΔCDM
nên \(\widehat{ABM}=\widehat{CDM}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
NH
9 tháng 8 2019
a, Xét △ABC có: \(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^o\)
\(\Rightarrow45^o+70^o+\widehat{ACB}=180^o\)
\(\Rightarrow\widehat{ACB}=65^o\)
b, Xét △ABM và △DCM
Có: MA = MD (giả thiết)
\(\widehat{AMB}=\widehat{CMD}\)(đối đỉnh)
\(BM=MC\)(M là trung điểm của BC)
=> △ABM = △DCM (c.g.c)
=> \(\widehat{ABC}=\widehat{MCD}\)(2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> AB // CD
c, Xét △IMB và △KMC
Có: \(\widehat{IMB}=\widehat{CMK}\) (đối đỉnh)
BM = MC (gt)
\(\widehat{ABC}=\widehat{MCD}\)(cmt)
=> △IMB = △KMC (g.c.g)
=> MI = MK (2 cạnh tương ứng)
Mà M nằm giữa I, K
=> M là trung điểm của IK
11 tháng 4 2023
a: Xét tứ giác ABCD co
M là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AB=CD và AB//CD
=>CD vuông góc AC
b: AB+BC=AB+AD>BD=2BM
c: góc ABM=góc CDB
mà góc CDB>góc CBM
nên góc ABM>góc CBM
7 tháng 4 2020
a) Xét ΔΔBMC và ΔΔDMA có:
BM = DM (gt)
BMCˆBMC^ = DMAˆDMA^ (đối đỉnh)
MC = MA (suy từ gt)
=> ΔΔBMC = ΔΔDMA (c.g.c)
=> BC = DA (2 cạnh tương ứng)
b) Vì ΔΔBMC = ΔΔDMA (câu a)
nên BCAˆBCA^ = CADˆCAD^ (2 góc t ư) và BC = DA (2 cạnh t ư)
Xét ΔΔDCA và ΔΔBAC có:
CA chung
CADˆCAD^ = ACBˆACB^ ( cm trên)
DA = BC (cm trên)
=> ΔΔDCA = ΔΔBAC (c.g.c)
=> DCAˆDCA^ = BACˆBAC^ = 90 độ (góc t ư)
Do đó CD ⊥⊥ AC
c) .................
7 tháng 4 2020
Giải
a) Xét ΔBMC và ΔDMA có:
BM = DM (gt)
BMC\(\widehat{BMC}\) = \(\widehat{DMA}\)(đối đỉnh)
MC = MA (suy từ gt)
=> ΔBMC = ΔDMA (c.g.c)
=> BC = DA (2 cạnh tương ứng)
b) Vì ΔBMC = ΔDMA (câu a)
nên \(\widehat{BCA}=\widehat{CAD}\)= \(\widehat{CAD}\)(2 góc t ư) và BC = DA (2 cạnh t ư)
Xét ΔDCA và ΔBAC có:
CA chung
\(\widehat{CAD}\)= \(\widehat{ACB}\)(cm trên)
DA = BC (cm trên)
=> ΔDCA = ΔBAC (c.g.c)
=> \(\widehat{DCA}\) = \(\widehat{BAC}\)= 90 \(^0\) (góc t ư)
Do đó CD ⊥ AC
c,Vì BN // AC (gt) => \(\widehat{BND}\)=\(\widehat{ACD}\)=90\(^0\)\(\widehat{BND}\)=\(\widehat{ACD}\)=90\(^0\)
Xét tam giác BND vuông tại N có:
NM là đường trung tuyến ứng vs cạnh huyền BD => NM=\(\frac{1}{2}\)BC=BM
Xét 2 tam giác vuông: ΔABM(\(\widehat{A}\)=90\(^0\))ΔABM(\(\widehat{A}\)=90\(^0\))và ΔCNM(\(\widehat{C}\)=90\(^0\))ΔCNM(\(\widehat{C}\)=90\(^0\)) có:
AM = CM (gt)
NM = BM (cmt)
=> ΔABM=ΔCNM(ch−1cgv) (đpcm)
# mui #
Dễ quá . Vì mình học lớp 8 rồi mà sao không để được