Chứng minh rằng trong một tam giác cân, hai đường cao ứng với hai cạnh bên thì bằng nhau ?
Giúp mk nhé các bn!!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 4 2018
Giả sử ΔABC cân tại A có hai đường trung tuyến BM và CN, ta cần chứng minh BM = CN.
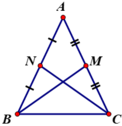
Ta có: AC = 2.AM, AB = 2. AN, AB = AC (vì ΔABC cân tại A)
⇒ AM = AN.
Xét ΔABM và ΔACN có:
AM = AN
AB = AC
Góc A chung
⇒ ΔABM = ΔACN (c.g.c) ⇒ BM = CN (hai cạnh tương ứng).
(Còn một số cách chứng minh khác, nhưng do giới hạn kiến thức lớp 7 nên mình xin sẽ không trình bày.)
16 tháng 2 2023
#\(N\)
`a,` `GT: AB = AC,` \(\widehat{B}=\widehat{C}\)
`CM: BB' = C``C'`
`BB'` là đường trung tuyến
`-> B'` là trung điểm của `AC`
`-> AB' = B'C`
`C``C'` là đường trung tuyến
`-> C'` là trung điểm của `AB`
`-> AC' = C'B`
Tam giác `ABC` cân tại `A`
`-> AB = AC`
`-> AC' = AB' = C'B = B'C`
Xét Tam giác `BB'C` và Tam giác `C``C'B:`
`C'B = B'C`
\(\widehat{B}=\widehat{C}\)
`BC` chung
`=>` Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`=> BB' = C``C' (2` cạnh tương ứng `) (đpcm)`
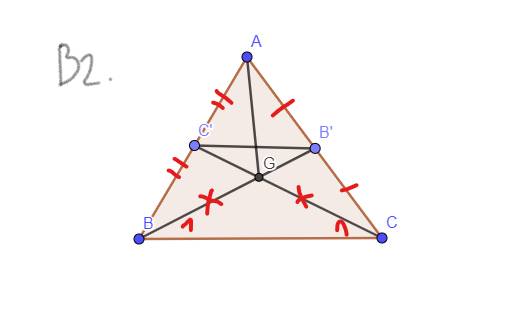
`b, GT: AB' = B'C ; AC'=C'B ; C``C' = BB'`
`KL:` Tam giác `ABC` cân
`BB', C``C'` là đường trung tuyến
giả sử: `BB'` cắt `C``C'` tại `G`
`-> G` là trọng tâm của Tam giác `ABC`
`-> GB = 2/3 BB'`
`-> GC = 2/3 C``C'`
`BB' = C``C' -> GB = GC`
`->` Tam giác `GBC` cân tại `G`
`->`\(\widehat{B_1}=\widehat{C_1}\)
Xét Tam giác `BB'C` và Tam giác `C``C'B` có:
`BB' = C``C'`
\(\widehat{B_1}=\widehat{C_1}\)
`BC` chung
`=>`Tam giác `BB'C =` Tam giác `C``C'B (c-g-c)`
`-> BC' = B'C`
`-> 1/2 AB = 1/2 AC`
`-> AB = AC`
`->` Tam giác `ABC` cân tại `A (đpcm)`.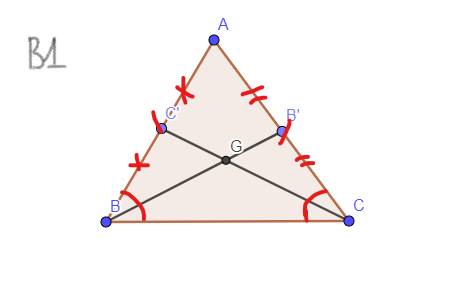
BN
3 tháng 4 2018
Bạn vẽ hình ra và gọi hai cạnh bên của tam giác cân đó lần lượt là AB, AC.
Gọi E, F lần lượt là trung điểm của các cạnh AB, AC.
Nối E, F với các đỉnh đối diện các cạnh AB, AC ta được 2 tam giac ABF, ACE
Ta có 2 tam giác trên bằng nhau theo trường hợp c.g.c
AB = AC
(Cạnh bên của tam giác cân)
Góc A chung AE = AF => cạnh BF = CE (là 2 đường trung tuyến ứng vói 2 cạnh bên của tam giác cân)
=>Đpcm
19 tháng 9 2023
Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)
\( \Rightarrow \)MA = MC = \(\dfrac{1}{2}\)AC; NA = NB = \(\dfrac{1}{2}\)AB
Vì \(\Delta ABC\) cân tại A nên AB = AC ( tính chất)
Do đó, AM = MC = NA = NB
Xét \(\Delta \)ANC và \(\Delta \)AMB, ta có:
AN = AM
\(\widehat A\) chung
AC = AB
\( \Rightarrow \)\(\Delta \)ANC = \(\Delta \)AMB (c.g.c)
\( \Rightarrow \) NC = MB ( 2 cạnh tương ứng)
Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.
Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) ( tính chất đường trung tuyến trong tam giác)
Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
+) \(BC\) là cạnh chung
+) \(CN = BM\) (giả thiết)
+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)
8 tháng 4 2015
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN (đpcm)
5 tháng 8 2017
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
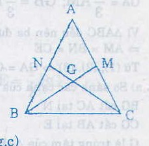
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
BN
18 tháng 4 2016
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Ta có AN = NB = AB/2 (Tính chất đường trung tuyến)
AM = MC = AC/2 (Tính chất đường trung tuyến)
Vì ∆ ABC cân tại A=> AB = AC nên AM = AN
Xét ∆BAM ;∆CAN có:
AM = AN (cm trên)
Góc A chung
AB = AC (∆ABC cân)
Nên suy ra ∆BAM = ∆CAN (c-g-c)
=> BM = CN ( 2 cạnh tương ứng)