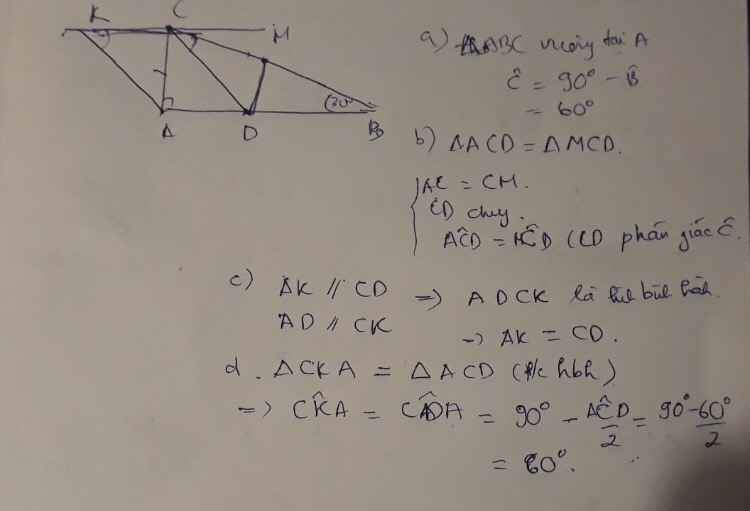
Cho tam giác ABC vuông tại A có B=30 độ a,Tính C b,Vẽ tia phân giác của góc C cắt cạnh AB tại D c,Trên cạnh CB lấy điểm M sao cho CM=CA.Chứng minh rằng:ACD=MCD d, tính AKC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình vẽ hình rồi, còn phần chứng minh làm như bạn Trần Hoàng Việt nha!!
a) Ta có : A=900 ; B=300
=> C=180-A-B=180-90-30=60
b) Xét tam giác ACD và MCD ta có :
CD chung (1)
CM=CA (gt)(2)
góc ACD=góc DCM (gt) (3)
Từ (1)(2)(3) =>\(\Delta\)ACD=\(\Delta\)MCD (c.g.c)
c) Ta có :AK//CD; CK//AD => tứ giác ADCK là hình bình hành
=>AK=CD (cặp cạnh tương ứng )
d)Ta có : \(\widehat{BDC}\)=180-30-60:2=1200
\(\widehat{CPA}\)=180-120=60
Do ADCK là hình bình hành nên \(\widehat{CPA}\)=\(\widehat{AKC}\)=\(60^0\)

a. Ta có A+B+C=180 độ ( tổng 3 góc trong tam giác)
=> C= 180 độ - ( A+B) =60 độ
b. Xét 2 tam giác vuông : tam giác : DCA và DCM có :
DC chung; góc DCA = góc DCM ( cd là phân giác của acm ); CM=CA (gt)
=>tam giác DCM=tam giác DCA (c.g.c)
c. xét hai tam giác vuông : DCA và KAC có :
AC chung; góc DCA = góc CAK ( so le trong vì DC // AK )
=> DCA=KAC(cgv. gn )=>AK=CD(2 góc tương ứng )
d. ta có: tam giác : DCA = KAC ( câu c)=>AKC=ADC (2 góc tương ứng)
Mà CAK+AKC+KCA=180 độ ( tổng 3 góc trong tam giác)
=>AKC= 180-90-30=60 độ
vì KAC=ACD60/2=30 độ

a, Xét ∆ABC vuông tại A có: B + C = 90o
=> 30o + C = 90o
=> C = 60o
b, Vì CD là tia phân giác của C
=> ACD = DCB = ACB/2 = 60o/2 = 30o
Xét ∆ACB và ∆MCD
Có: AD: cạnh chung (gt)
ACD = DCM (vì CD là tia p/g của C)
CA = CM (gt)
=> ∆ACB = ∆MCD (c.g.c)
c, XY vuông góc CA => KCA = 90o
Vì AK // CD => CKA = CDA (2 góc so le trong)
Xét ∆CAK vuông tại C và ∆ADC vuông tại A
Có: CA: cạnh chung
CKA = CDA (cmt)
=> ∆CAK = ∆ADC (cgv-gn)
=> AK = DC (2 cạnh tương ứng)
d, Vì ∆CAK = ∆ADC (câu c)
=> KAC = ACD (2 góc tương ứng)
Mà ACD = 30o
=> KAC = 30o
Xét ∆KAC vuông tại C có: KAC + AKC = 90o
=> 30o + AKC = 90o
=> AKC = 60o

mk ko rảnh cho lắm nên bạn nhấn link mà tra nha![]()
https://olm.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+t%E1%BA%A1i+A+c%C3%B3+g%C3%B3c+B+=+30+%C4%91%E1%BB%99+.a)+T%C3%ADnh+g%C3%B3c+C+b)+v%E1%BA%BD+tia+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+C+c%E1%BA%AFt+c%E1%BA%A1nh+AB+t%E1%BA%A1i+D+.+Tr%C3%AAn+c%E1%BA%A1nh+CB+l%E1%BA%A5y+%C4%91i%E1%BB%83m+M+sao+cho+CM+=+CA+.+CMR+:+tam+gi%C3%A1c+ACD+=+tam+gi%C3%A1c+MCD+.Qua+C+v%E1%BA%BD+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+xy+vu%C3%B4ng+g%C3%B3c+CA+.+T%E1%BB%AB+A+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+//+vs+CD+c%E1%BA%AFt+xy+%E1%BB%9F+K+.+Cm+:+AK+=+CDc)+t%C3%ADnh+g%C3%B3c+AKC+&id=990903

a) Ta có: \(BC^2=13^2=169\)
\(AB^2+AC^2=5^2+12^2=169\)
Do đó: \(BC^2=AB^2+AC^2\)(=169)
Xét ΔABC có \(BC^2=AB^2+AC^2\)(cmt)
nên ΔABC vuông tại A(Định lí Pytago đảo)