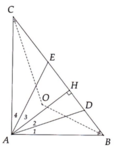
cho tam giác ABC Vuông tại A Kẻ Ah vuông B( H thuộc BC) Tia phân giác góc HAC cách BC tại D chứng minh Tam Giác ABD CÂN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CU
17 tháng 2 2019
chị tự kẻ hình :
AH _|_ BC (gt) => góc DHA = 90o (đn)
=> góc ADH + góc DHA + góc DAH = 180 (đl)
=> góc ADH + 90 + góc DAH = 180
=> góc ADH = 180 - 90 - góc DAH
=> góc ADH = 90 - góc DAH (1)
có tam giác ABC vuông tại A (gt)
=> góc DAB + góc CAD = 90
=> góc DAB = 90 - góc CAD (2)
AD là phân giác của góc HAC (gt) => góc CAD = góc DAH (đn) (3)
(1)(2)(3) => góc DAB = góc ADB
=> tam giác ABD cân tại B (dh)
17 tháng 2 2019
Ta có: \(\widehat{CAD}=\widehat{BAC}-\widehat{BAD}=90^0-\widehat{BAD}\)
\(\widehat{HAD}=90^0-\widehat{BDA}\)
Mà \(\widehat{CAD}=\widehat{HAD}\) (vì AD là tia phân giác của góc HAC)
Do đó: \(\widehat{BAD}=\widehat{BDA}\Rightarrow\Delta ABD\) cân tại B
Chúc bạn học tốt.
DK
24 tháng 6 2020
Bài làm:
a, Áp dụng đl Pythagoras vào ∆ABC vuông tại A có
BC² = AB² + AC²
=> BC² = 6² + 8²
=> BC² = 100
=> BC = √100 = 10(cm) (do BC> 0)
b, Ta có DH ⊥ BC (gt)
=> BHD = CHD = 90°
Xét ∆ABD vuông tại A và ∆HBD vuông tại H có
BD : chung
ABD = CBD (BD là pg ABC - gt)
=>∆ABD = ∆HBD (ch-gn)
=> AD = DH (2 cạnh t/ứ)
c, Xét ∆DHC vuông tại H có
DC > HD (ch > cgv)
Mà HD = AD (cmt)
=> DC > AD
d, Ta có BAC +KAC = 180° (kề bù)
=> 90° + KAC = 180°
=> KAC = 90°
Lại có : KB = BC (gt)
AB = BH (∆ABD = ∆HBD)
=> KB - AB = BC - BH
=> AK = CH
Xét ∆AKD vuông tại A và ∆HCD vuông tại H có
AK = CH (cmt)
AD = HD (cmt)
=>∆AKD = ∆HCD (2 cgv)
=> ADK = HDC (2 góc t/ứ)
Mặt khác ta có
ADH + HDC = 180° (kề bù)
=> ADK + ADH = 180°
=> KDH = 180°
=> K,D,H thẳng hàng
16 tháng 4 2022
a: Xét ΔABC có AB<AC
mà BH là hình chiếu của AB trên BC
và CH là hình chiếu của AC trên BC
nên HB<HC
Ta có:AB<AC
nên \(\widehat{B}>\widehat{C}\)
hay \(\widehat{BAH}< \widehat{CAH}\)
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{CAD}=\widehat{HAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
hay ΔBDA cân tại B
6 tháng 1 2016
Ta có Góc BDA + Góc HAD = 90 độ ( 1 )
Lại có Góc BAD + Góc DAC = 90 độ ( 2 )
Mà AD là tia phân giác của góc HAC
->Góc HAD = Góc DAC ( 3 )
Từ ( 1 ) ( 2 ) ( 3 )
->Góc BAD = Góc BDA
Xét tam giác ABD có
Góc BAD = Góc BDA
-> Tam giác ABD là tâm giác cân tại B
