Cho tam giác DEF, M thuộc EF. Vẽ MP song song với DE, MN song song vs DF. Chứng minh rằng
A) NMPD là hình bình hành
B) tìm điều kiện của tam giác DEF để NMPD là hình chữ nhật
C) tìm điều kiện của tam giác DEF và M để NMPD là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này tương tự bài 1
a) EF = 15
=> DM = EM = FM = 7,5
b) MND + D = 180
MND + 90 = 180
=> MND = 90
D + MED = 180
90 + MED = 180
=> MED = 90
=> DNME là hình chữ nhật
c) y hệt như bài trước mik giải

\(\text{#TNam}\)
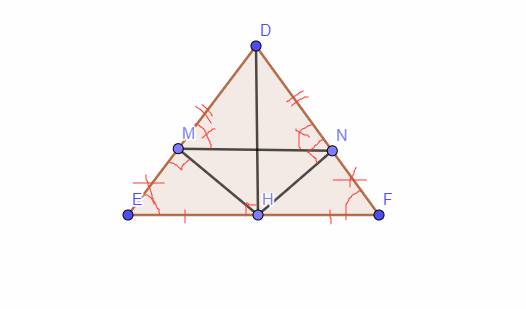
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`

a: Xét tứ giác AEDF có
AE//DF
AF//DE
Do đó: AEDF là hình bình hành
b: Để AEDF là hình thang vuông thì góc A=90 độ

bạn tự vẽ hình nha!Nên sửa DQEF thành DQEP.
a,tứ giác DQEP có:ME=MD,MQ=MP nên DQEP là hình bình hành.
Lại có:DE vuông góc với QP nên hình bình hành DQEP là hình thoi.
b,DQEP là hình thoi nên EP song song với DQ mà FK song song với PE nên DQ song song với FK(1)
Lại có:DF và QK cùng vuông góc với DM nên DF song song với QK(2).
Từ (1) và (2) suy ra DFKQ là hình bình hành

Bài 2:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trug điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: Để AMCK là hình vuông thì AM=CM
=>AM=BC/2
=>ΔABC vuông tại A
pn tự vẽ hình nhak
a, có MP // DE (GT) suy ra MP // DN ( N thuộc DF )
MN // DF (GT) suy ra MN // DP ( P thuộc DF )
Suy ra tứ giác NMPD là hình bình hành ( dấu hiệu nhận biết các cạnh đối // )
b, ( cm ngược lại nhak )
có tứ giác NMPD là HCN suy ra góc NDB = 90 độ
suy ra tam giác DEF vuông tại D
Vậy nếu tam giác DEF vuông tại D thì tứ giác NMPD là HCN
c, có tứ giác NMPD là HV suy ra DM là tia phân giác của góc D ứng vs cạnh EF
Vậy nếu DM là tia phân giác của góc D thì tứ giác MNPD là HV
<<< mk lm v có j sai sót pn góp ý dùm mk nhak >>>