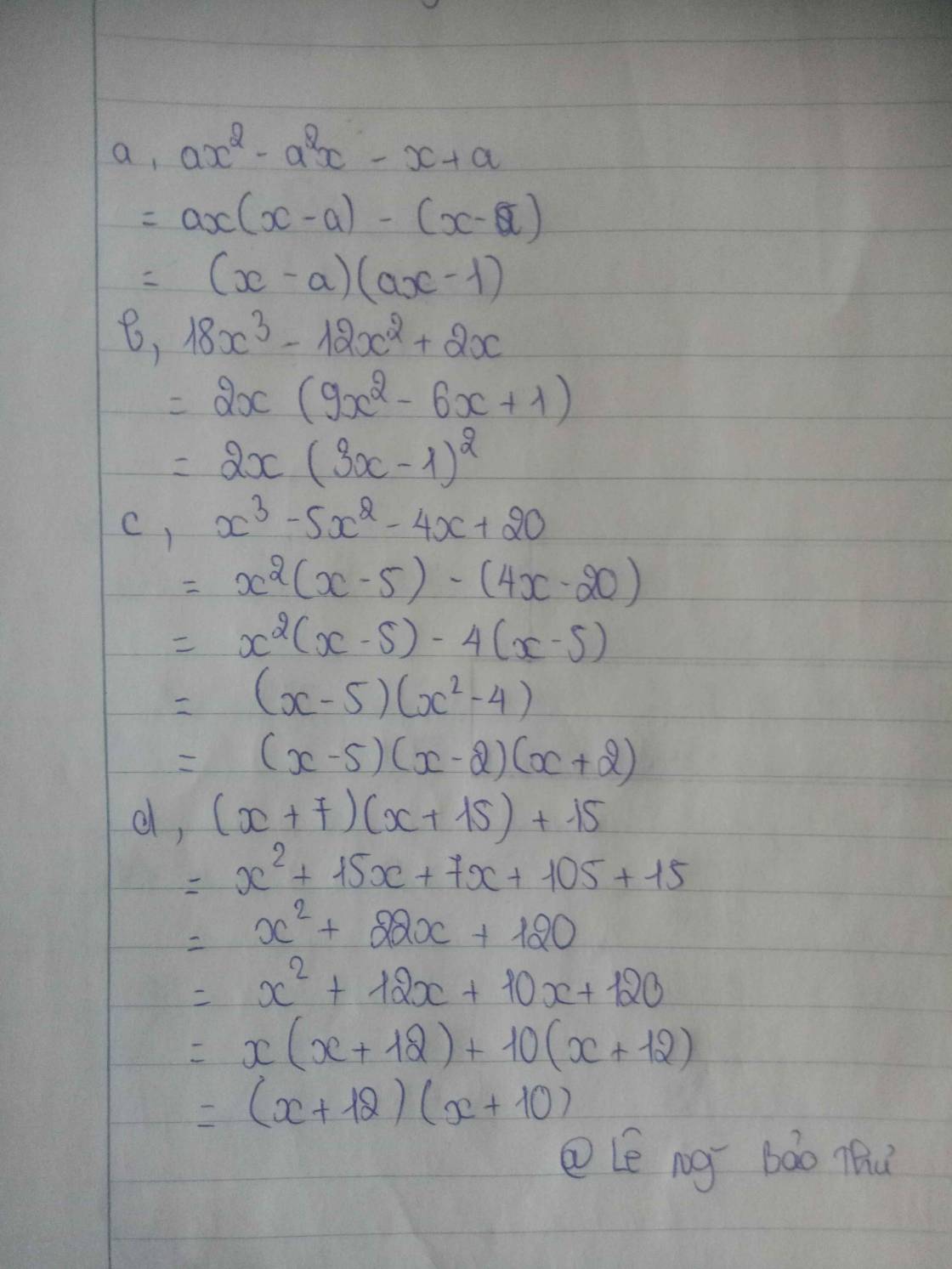Phân tích thành nhân tử 5x(x-7)(x+7)-x(2x-1)^2-(x^3+4x^2-246x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 11 2021
Bài 1:
a) \(7x^2\left(x^2-5x+1\right)=7x^4-35x^3+7x^2\)
b) \(\left(2x-3\right)\left(x+7\right)=2x^2+11x-21\)
Bài 2:
a) \(4x^2y-8x^3y^2=4x^2y\left(1-2xy\right)\)
b) \(2x-4y-ax+2ay=x\left(2-a\right)-2y\left(2-a\right)=\left(2-a\right)\left(x-2y\right)\)
LM
28 tháng 5 2017
1. a) 7x2 - 5x - 2 = 7x2 - 7x + 2x - 2 = 7x(x - 1) + 2(x - 1) = (x - 1).(7x + 2)
2. 5(2x - 1)2 - 3(2x - 1) = 0
<=> (2x - 1).[5(2x - 1) - 3] = 0
<=> (2x - 1).(10x - 8) = 0
<=> (2x - 1) = 0 hoặc (10x - 8) = 0
<=> x = 1/2 hoặc x = 4/5
3. x2 - 4x + 7 = (x2 - 4x + 4) + 3 = (x - 2)2 + 3
Do: (x - 2)2 > hoặc = 0 (với mọi x)
Nên (x - 2)2 + 3 > hoặc = 3 (với mọi x)
Hay (x - 2)2 + 3 > 0 (với mọi x) => đpcm
29 tháng 1 2023
\(a.\) \(ax^2-a^2x-x+a\)
\(=\left(ax^2-a^2x\right)-\left(x-a\right)\)
\(=ax\left(x-a\right)-\left(x-a\right)\)
\(=\left(ax-1\right)\left(x-a\right)\)
\(b.\) \(18x^3-12x^2+2x\)
\(=2x\left(9x^2-6x+1\right)\)
\(=2x\left(3x-1\right)^2\)
\(c.\) \(x^3-5x^2-4x+20\)
\(=\left(x^3-5x^2\right)-\left(4x-20\right)\)
\(=x^2\left(x-5\right)-4\left(x-5\right)\)
\(=\left(x^2-4\right)\left(x-5\right)\)
\(=\left(x-2\right)\left(x+2\right)\left(x-5\right)\)
\(d.\) \(\left(x+7\right)\left(x+15\right)+15\)
\(=x^2+15x+7x+105+15\)
\(=x^2+22x+120\)
\(=\left(x+10\right)\left(x+12\right)\)
6 tháng 10 2021
\(1)4x^2-25+\left(2x+7\right).\left(5.2x\right)\)
\(=\left(2x\right)^2-5^2-\left(2x+7\right).\left(2x-5\right)\)
\(=\left(2x.5\right)\left(2x+5\right).\left(2x+7\right)\left(2x-5\right)\)
\(=\left(2x-5\right)\left(2x+5-2x+7\right)\)
\(=\left(2x-5\right).12\)
\(2)3x+4-x^2-4x\)
\(=3(x+4)-\left(x+4\right)\)
\(=\left(3-x\right)\left(x+4\right)\)
\(3)5x^2-2y^2-10x+10y\)
\(=5\left(x^2-y^2\right)-10\left(x-4\right)\)
\(=5\left(x-y\right)\left(x+y\right)-10\left(x-y\right)\)
\(=\left(x-y\right)[5(x+y)-10]\)
Còn lại bn lm nốt nha!
29 tháng 10 2021
a) \(2x\left(x-7\right)-5y\left(x-7\right)=\left(x-7\right)\left(2x-5y\right)\)
b) \(5x^3y+10x^2y+5xy=5xy\left(x^2+2x+1\right)=5xy\left(x+1\right)^2\)
c) \(4y^2-4y-x^2+1=\left(2y-1\right)^2-x^2=\left(2y-1-x\right)\left(2y-1+x\right)\)
d) \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1=\left(x^2+3x+1\right)^2\)
29 tháng 10 2021
a: \(=\left(x-7\right)\left(2x-5y\right)\)
b: \(=5xy\left(x^2+2x+1\right)=5xy\left(x+1\right)^2\)
14 tháng 10 2020
1) 4x2 + 5x - 6 = 4x2 + 8x - 3x - 6 = 4x( x + 2 ) - 3( x + 2 ) = ( x + 2 )( 4x - 3 )
2) 5x2 - 18x - 8 = 5x2 - 20x + 2x - 8 = 5x( x - 4 ) + 2( x - 4 ) = ( x - 4 )( 5x + 2 )
3) 2x2 + 3x - 27 = 2x2 - 6x + 9x - 27 = 2x( x - 3 ) + 9( x - 3 ) = ( x - 3 )( 2x + 9 ) < đã sửa ._. >
4) 7x2 + 3xy - 10y2 = 7x2 - 7xy + 10xy - 10y2 = 7x( x - y ) + 10y( x - y ) = ( x - y )( 7x + 10y )
5) x2 + 5x - 2 < sai đề ._. >
6) x8 + x7 + 1 = x8 + x7 + x6 - x6 + 1
= ( x8 + x7 + x6 ) - ( x6 - 1 )
= x6( x2 + x + 1 ) - ( x3 - 1 )( x3 + 1 )
= x6( x2 + x + 1 ) - ( x - 1 )( x2 + x + 1 )( x3 + 1 )
= ( x2 + x + 1 )[ x6 - ( x - 1 )( x3 + 1 ) ]
= ( x2 + x + 1 )( x6 - x4 + x3 - x + 1 )
H
21 tháng 8 2021
Phân tích đa thức thành nhân tử(tách hạng tử)
1)x^2+2x-3=x^2-x+3x-3=x(x-1)+3(x-1)=(x-1)(x+3)
2)x^2-5x+6=x^2-2x-3x+6=x(x-2)-3(x-2)=(x-2)(x-3)
3)x^2+7x+12=(x+3)(x+4)
4)x^2-x-12=(x-4)(x+3)
5)3x^2+3x-36=3[(x-3)(x+4)]
6)5x^2-5x-10=5[(x-2)(x+1) ]
7)3x^2-7x-6=(x-3)(3x+2)
8)4x^2+4x-3=4x^2+6x-2x-3=(2x-1)(2x+3)
9)8x^2-2x-3=8x^2+4x-6x-3=(4x-3)(2x+1)
21 tháng 8 2021
1: \(x^2+2x-3=\left(x+3\right)\left(x-1\right)\)
2: \(x^2-5x+6=\left(x-2\right)\left(x-3\right)\)
3: \(x^2+7x^2+12x=4x\left(2x+3\right)\)
4: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)
5: \(3x^2+3x-36=3\left(x^2+x-12\right)=3\left(x+4\right)\left(x-3\right)\)
6: \(5x^2-5x-10=5\left(x^2-x-2\right)=5\left(x-2\right)\left(x+1\right)\)