4.x - 128= 23.32
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CC
21 tháng 2 2020
\(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128=0\)
\(\Leftrightarrow x\left(x+10\right)\left(x+4\right)\left(x+6\right)+128=0\)
\(\Leftrightarrow\left(x^2+10x\right)\left(x^2+10x+24\right)+128=0\)
Đặt \(x^2+10x+12=t\)
\(\Rightarrow\left(t-12\right)\left(t+12\right)+128=0\)
\(\Leftrightarrow t^2-144+128=0\)\(\Leftrightarrow t^2-16=0\)
\(\Leftrightarrow\left(t-4\right)\left(t+4\right)=0\)\(\Leftrightarrow\left(x^2+10x+12-4\right)\left(x^2+10x+12+4\right)=0\)
\(\Leftrightarrow\left(x^2+10x+8\right)\left(x^2+10x+16\right)=0\)
\(\Leftrightarrow\left(x^2+10x+8\right)\left(x+2\right)\left(x+8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-8\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{-8;-2\right\}\)
21 tháng 2 2020
Ta có : \(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128=0\)
\(\Leftrightarrow\left(x^2+10x\right)\left(x^2+10x+24\right)+128=0\) (2)
Đặt \(x^2+10x=t\) Khi đó pt (2) có dạng :
\(t\cdot\left(t+24\right)+128=0\)
\(\Leftrightarrow t^2+24t+128=0\)
\(\Leftrightarrow\left(t+12\right)^2-16=0\)
\(\Leftrightarrow\left(t+12-4\right)\left(t+12+4\right)=0\)
\(\Leftrightarrow\left(t+8\right)\left(t+16\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}t+8=0\\t+16=0\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}t=-8\\t=-16\end{cases}}\)
+) Với \(t=-8\) thì \(x^2+10x=-8\)
\(\Leftrightarrow\left(x+5\right)^2=17\)
\(\Leftrightarrow\orbr{\begin{cases}x+5=\sqrt{17}\\x+5=-\sqrt{17}\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}x=-5+\sqrt{17}\\x=-5-\sqrt{17}\end{cases}}\) ( thỏa mãn )
+) Với \(t=-16\) thì \(x^2+10x=-16\)
\(\Leftrightarrow\left(x+5\right)^2-9=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+14\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x+14=0\end{cases}}\) \(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-14\end{cases}}\) ( thỏa mãn )
Vậy : phương trình đã cho có tập nghiệm \(S=\left\{-5\pm\sqrt{17},4,-14\right\}\)
6 tháng 10 2021
\(\sqrt{\dfrac{72x}{128}}=\dfrac{3}{4}\)
\(\Leftrightarrow x\cdot\dfrac{9}{16}=\dfrac{9}{16}\)
hay x=1
B
11 tháng 3 2022
3Fe+2O2-to>Fe3O4
\(\dfrac{16}{7}\)----\(\dfrac{32}{21}\)
n Fe=\(\dfrac{128}{56}\)=\(\dfrac{16}{7}\)mol
=>VO2=\(\dfrac{32}{21}\).22,4=34,13l
CM
11 tháng 3 2019
+) Ta có; 8+x3 = (2 + x).( 4 - 2x+ x2 )
Mà 4 - 2x + x2 = (1 – 2x + x2 ) + 3 = ( 1- x)2 + 3 >0 với mọi x.
Do đó: 8 + x3 ≠ 0 ⇔ 2 + x ≠ 0 ⇔ x ≠ -2
+) Điều kiện xác định: x ≠ -2.
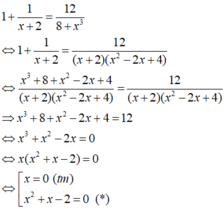
Giải phương trình (*):
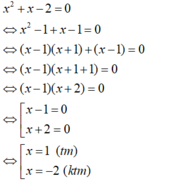
Vậy tập nghiệm của phương trình là S = {0; 1}.
NT
1
15 tháng 8 2021
a: Ta có: \(814-\left(x-305\right)=712\)
\(\Leftrightarrow x-305=102\)
hay x=407
b: Ta có: \(2x-138=2^3\cdot2^2\)
\(\Leftrightarrow2x=32+138=170\)
hay x=85
c: Ta có: \(20-\left[7\left(x-3\right)+4\right]=2\)
\(\Leftrightarrow7\left(x-3\right)+4=18\)
\(\Leftrightarrow7\left(x-3\right)=14\)
\(\Leftrightarrow x-3=2\)
hay x=5
GL
4
25 tháng 7 2018
lớp 9 ? mà ko làm dc bài này ?
\(x^2+2.14+196-128-196=0.\)
\(\left(x+14\right)^2-324=0\)
\(\left(x+14\right)^2-18^2=0\)
\(\hept{\begin{cases}\left(x+14+18\right)=0\\\left(x+14-18\right)=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-14-18\\x=-14+18\end{cases}}\)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
NN
4
1 tháng 2 2019
CÁCH KHÁC:
\(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128\)
\(<=>x\left(x+10\right)\left(x+4\right)\left(x+6\right)+128\)
\(<=>\left(x^2+10x\right)\left(x^2+10x+24\right)+128\)
\(<=>\left(x^2+10x\right)^2+24\left(x^2+10x\right)+128\)
\(<=>\left(x^2+10x\right)^2+2.\left(x^2+10x\right).12+12^2-16\)
\(<=>\left(x^2+10x+12\right)^2-4^2\)
\(<=>\left(x^2+10x+12-4\right) \left(x^2+10x +12+4\right)\)
\(<=>\left(x^2+10x+8\right)\left(x^2+10x+16\right)\)
\(<=>\left(x^2+10x+8\right)\left(x^2+2x+8x+16\right)\)
\(<=>\left(x^2+10x+8\right)\left[x\left(x+2\right)+8\left(x+2\right)\right]\)
\(<=>\left(x^2+10x+8\right)\left(x+2\right)\left(x+8\right)\)
\(< =>\left[{}\begin{matrix}x^2+10x+8=0\\x+2=0\\x+8=0\end{matrix}\right.< =>\left[{}\begin{matrix}x=-5+\sqrt{17}\\x=-5-\sqrt{17}\\x=-2\\x=-8\end{matrix}\right.\)
Vậy...
KB
1 tháng 2 2019
Ta có :
\(x\left(x+4\right)\left(x+6\right)\left(x+10\right)+128=0\)
\(\Leftrightarrow\left[x\left(x+10\right)\right]\left[\left(x+4\right)\left(x+6\right)\right]+128=0\)
\(\Leftrightarrow\left(x^2+10x\right)\left(x^2+10x+24\right)+128=0\)
\(\Leftrightarrow\left(x^2+10x\right)^2+24\left(x^2+10x\right)+128=0\)
\(\Leftrightarrow\left(x^2+10x\right)^2+24\left(x^2+10x\right)+144=16\)
\(\Leftrightarrow\left(x^2+10x+12\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+10x+12=4\\x^2+10x+12=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left(x+5\right)^2-13=4\\\left(x+5\right)^2-13=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+5\right)^2=17\\\left(x+5\right)^2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+5=\pm\sqrt{17}\\x+5=\pm3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\sqrt{17}-5\\\left[{}\begin{matrix}x=-2\\x=-8\end{matrix}\right.\end{matrix}\right.\)
`4x - 128 = 2^3 . 3^2`
`=> 4x - 128 = 8 .9`
`=> 4x - 128 = 72`
`=> 4x = 72 + 128`
`=> 4x = 200`
`=> x = 200 : 4`
`=> x = 50`
Vậy ...
4x -128 = 23 .32
4x-128=8 . 9
4x-128=72
4x = 72 +128
4x = 200
x = 200 : 4
x = 50
Vậy x = 50