Cho đường tròn $(O;R)$ và một dây cung $AB$ sao cho số đo cung lớn $AB$ gấp đôi số đo cung nhỏ $AB$. Tính độ dài dây $AB$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 4 2017
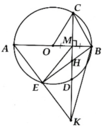
a, Chứng minh được ∆COD đều => A M B ^ = 60 0
b, A B C ^ = 30 0 => A O C ^ = 60 0 => l A C ⏜ = πR 3
CM
21 tháng 5 2017
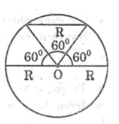
Vì hai cung không phải là cung lớn nên nó có thể là cung nhỏ hoặc cung nửa đường tròn
Cung nửa đường tròn có số đo bằng 180 ° và dây căng cung bằng 2R
Cung 60 ° có dây căng cung là R
Vậy cung nửa đường tròn và cung 60 ° thỏa mãn bài toán
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
a. Câu hỏi chưa rõ ràng
b. Vì số đo cung nhỏ AB bằng một nửa số đo cung lớn AB mà tổng số
đo 2 cung bằng $360^0$ nên số đo cung nhỏ $AB$ là $120^0$
Từ $O$ kẻ $OH\perp AB$ như hình. Tam giác $OAB$ cân tại $O$ nên đường cao $OH$ đồng thời là đường phân giác, trung tuyến.
Do đó: $\widehat{AOH}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.120^0=60^0$
$\frac{AH}{AO}=\sin \widehat{AOH}=\sin 60^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AH=\frac{\sqrt{3}}{2}AO=\frac{\sqrt{3}}{2}R$
$\Rightarrow AB=2AH=\sqrt{3}R$
2 tháng 7 2023
a: sđ cung AnB=360-80=280 độ
b: Độ dài cung là; \(\dfrac{2\cdot pi\cdot3\cdot80}{360}=\dfrac{4}{3}\cdot pi\)
c: C=3*2*3,14=18,84(cm)
S=3^2*3,14=28,26cm2
CM
2 tháng 6 2017
a, A n B ⏜ - cung lớn; A m B ⏜ - cung nhỏ
Vì sđ A n B ⏜ + sđ A m B ⏜ = 360 0 ; mà sđ A n B ⏜ = 3sđ A m B ⏜
nên sđ A n B ⏜ = 270 0 và độ dài cung A n B ⏜ là l = 3 πR 2
b, Vì DOAB vuông cân => A O B ^ = 90 0 và O A B ^ = O B A ^ = 45 0
c, Vì AB = R 2 => OH = R 2 2 (OH ⊥ AB; H ∈ AB)
Gọi x là số đo cung nhỏ AB (x > 0)
Số đo cung lớn AB là 2x
Ta có:
x + 2x = 360⁰
3x = 360⁰
x = 360⁰ : 3
x = 120⁰
⇒ ∠AOB = 120⁰
∆AOB có:
OA = OB = R
⇒ ∆AOB cân tại O
⇒ ∠OAB = ∠OBA = (180⁰ - ∠AOB) : 2
= (180⁰ - 120⁰) : 2
= 30⁰
Ta có hình vẽ sau:
Vẽ đường cao OH của ∆OAB
⇒ ∆OAH vuông tại H
⇒ cosOAH = AH : OA
⇒ AH = OA.cosOAH
= R.cos30⁰
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2AH