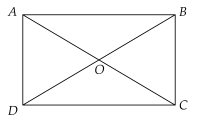
Tìm các góc đối đỉnh trong hình vẽ dưới đây:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
2
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
2 góc ở hình 3.6.b là hai góc đối đỉnh vì 2 góc này có mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
23 tháng 9 2017
a.
=> xOy+yOz=180'
=>2yOz+yOz=!80'
=>3yOz=180'
=>yOz=180':3
=>yOz=60'
b.
=>xOy'=yOz=60'(2 góc đối đỉnh)
c.
Các cặp góc đối đỉnh trong hình là: xOy' và yOz, y'Oz và xOy
23 tháng 9 2017
bài của mình thiếu 2 góc kề bù ỏ phần giải thích câu a bạn sửa lại giùm nha!
GH
Gia Hân
VIP
7 tháng 8 2023
a) Số đo \(\widehat{xAy}\) là: 90o vì có kí hiệu vuông góc.
b) Số đo \(\widehat{x'Ay}\):
Vì \(\widehat{x'Ay}\) và \(\widehat{xAy}\) là hai góc kề bù nên
nên \(\widehat{x'Ax}\) = \(\widehat{x'Ay}\) + \(\widehat{xAy}\)
180o = \(\widehat{x'Ay}\) + 90o
\(\widehat{x'Ay}\) = 180o - 90o
\(\widehat{x'Ay}\) = 90o
c) Số đo \(\widehat{x'Ay'}\):
Vì \(\widehat{xAy}\) và \(\widehat{x'Ay'}\) là hai góc đối đỉnh
nên: \(\widehat{x'Ay'}\) = \(\widehat{xAy}\) = 90o
d) Số đo \(\widehat{xAy'}\):
Vì \(\widehat{xAy'}\) và \(\widehat{x'Ay}\) là hai góc đối đỉnh
nên \(\widehat{xAy'}\) = \(\widehat{x'Ay}\) = 90o
NT
1
HQ
Hà Quang Minh
Giáo viên
29 tháng 11 2023
Hình tứ giác ABCD có 4 đỉnh, 4 cạnh và 4 góc.
+ 4 đỉnh là: A, B, C, D
+ 4 cạnh là: AB, BC, CD, DA
+ 4 góc là: Góc đỉnh A, cạnh AD và AB; Góc đỉnh B, cạnh BA và BC; Góc đỉnh C, cạnh CD và CB; Góc đỉnh D, cạnh DA và DC.
Hình tam giác KIL có 3 đỉnh, 3 cạnh và 3 góc.
+ 3 đỉnh là: K, I, L
+ 3 cạnh là: IK, KL, LI
+ 3 góc là: Góc đỉnh I, cạnh IL và IK; Góc đỉnh L, cạnh LK và LI; Góc đỉnh K, cạnh KL và LI
Hình tam giác EGH có 3 đỉnh, 3 cạnh và 3 góc.
+ 3 đỉnh là: E, G, H
+ 3 cạnh là: EG, GH, HE
+ 3 góc là: Góc đỉnh G, cạnh GH và GE; Góc đỉnh H, cạnh HG và HE; Góc đỉnh E, cạnh EG và EH.
Hình tam giác MNPQ có 4 đỉnh, 4 cạnh và 4 góc.
+ 4 đỉnh là: M, N, P, Q
+ 4 cạnh là: MN, NP, PQ, QM
+ 4 góc là: Góc đỉnh M, cạnh MN và MQ; Góc đỉnh Q, cạnh QM và QP; Góc đỉnh P cạnh PQ và PN; Góc đỉnh N, cạnh NM và NP.
Các cặp góc đối đỉnh trong hình:
\(\widehat{AOB}\) và \(\widehat{COD}\)
\(\widehat{AOD}\) và \(\widehat{COB}\)
Các cặp góc đối đỉnh trong hình vẽ trên là:
\(\widehat{AOB}\) và \(\widehat{COD}\)
\(\widehat{AOD}\) và \(\widehat{COB}\)