(0,5 điểm)
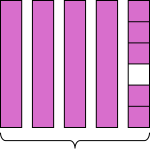
Viết hỗn số chỉ phần đã tô màu trong các hình...
Đọc tiếp
(0,5 điểm)
Viết hỗn số chỉ phần đã tô màu trong các hình sau.
a)
 |
|
| ................................... |
b)
 |
| ................................... |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DP
5
Những câu hỏi liên quan
24 tháng 2 2021
a)
H1: \(\dfrac{3}{4}\)
H2: \(\dfrac{2}{5}\)
H3: \(\dfrac{5}{8}\)
H4: \(\dfrac{3}{8}\)
b)
H1: \(1\dfrac{1}{4}\)
H2: \(2\dfrac{3}{4}\)
H3: \(3\dfrac{2}{3}\)
H4: \(4\dfrac{1}{2}\)
24 tháng 2 2021
a)
Hình 1: \(\dfrac{3}{4}\)
Hình 2: \(\dfrac{2}{5}\)
Hình 3: \(\dfrac{5}{8}\)
Hình 4: \(\dfrac{3}{8}\)
11 tháng 8 2020
Bg
F0: (thêm tâm O vào nũa và tô màu hình tròn nhỏ:))
Và bạn cũng tự thay vào các con số như đường kính AB là 40 cm, rồi sau đó tự tính, lúc đó, kết quả là tỉ số giữa diện tích của phần tô màu và phần không tô màu là \(\frac{1}{16}\)
F1: Phức tạp hơn xíu à:
Ta có: OA là đường kính của hình tròn nhỏ, AB là đường kính hình tròn lớn và OA x 2 = AB
=> Diện tích hình tròn nhỏ = (AB : 2 : 2) x (AB : 2 : 2) x 3,14
= (AB : 4) x (AB : 4) x 3,14
=> Diện tích hình tròn lớn = AB x AB x 3,14
=> Tỉ số diện tích của phần tô màu và phần không tô màu là \(\frac{\left(AB\div4\right)\times\left(AB\div4\right)\times3,14}{AB\times AB\times3,14}\)
= \(\frac{AB\div4\times AB\div4}{AB\times AB}\)
= \(\frac{AB\times AB\div4\div4}{AB\times AB}\)
= \(\frac{AB\times AB\times\frac{1}{16}}{AB\times AB}\)
= \(\frac{1}{16}\)
PT
1
CM
6 tháng 1 2018
Quan sát hình vẽ ta thấy có tất cả 1 hình tròn được tô màu toàn bộ, 1 hình tròn chia làm 4 phần và được tô màu 3 phần.
Vậy hỗn số chỉ phần đã tô màu trong hình là 1 3 4
Đáp án D
PT
1
CM
21 tháng 2 2017
Gọi diện tích được tô màu ở mỗi bước là 
Dễ thấy dãy các giá trị
u
n
là một cấp số nhân với số hạng đầu
u
1
=
4
9
và công bội q =
1
9
Gọi
S
k
là tổng của k số hạng đầu trong cấp số nhân đang xét thì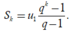 
Để tổng diện tích phần được tô màu chiếm 49,99% khi và chỉ khi
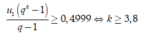
Vậy cần ít nhất 4 bước. Chọn B.
a) Hỗn số: `4`` 5/6 `
b) Hỗn số: `2`` 3/8`
\(3\dfrac{5}{6}\)\(2\dfrac{3}{8}\)