Cho hình chóp S.ABC có SA vuông góc với đáy và AB vuông góc với BC,gọi I là trung điểm BC.Tính góc giữa 2 mặt phẳng (SBC) và (ABC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

A
Admin
Giáo viên
31 tháng 3 2016
S A B C M
Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)

11 tháng 4 2023
\(SA\perp\left(ABC\right)\left(gt\right)\)
\(\Rightarrow SA\perp AB;SA\perp BC\)
Mặt khác: \(AB\perp BC\Rightarrow BC\perp SB\)
Vậy góc giữa (SBC) Và đáy là góc: \(\widehat{SBA}=\alpha\)
Trong tam giác vuông \(SBA\) ta có:
\(\tan\left(\alpha\right)=\dfrac{SA}{AB}=\dfrac{\sqrt{3}}{1}=\sqrt{3}\)
\(\Rightarrow\alpha=60^o\)

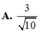
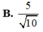
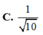
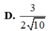

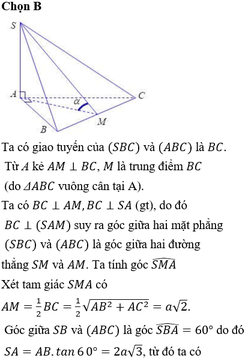
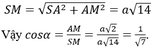
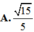
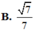
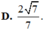
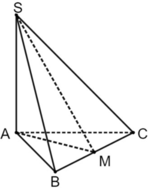
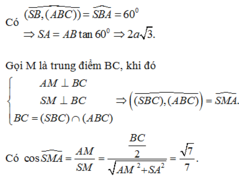
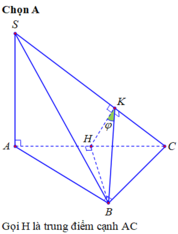

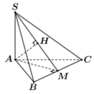
Ta có: \(\left(SBC\right)\cap\left(ABC\right)=BC\)
Mà lại có: \(SA\perp BC\left(SA\perp\left(ABCD\right)\right);AB\perp BC\)
Do đó \(BC\perp\left(SAB\right)\)
Mặt khác \(\left(SAB\right)\cap\left(ABCD\right)=AB;\left(SAB\right)\perp\left(SBC\right)=SB\)
Vậy \(\left(\left(SBC\right),\left(ABC\right)\right)=\left(SB,AB\right)=\widehat{SBA}\)