một vật chuyển động thẳng đều cứ sau mỗi giây tốc độ của vật tăng them 5 m/s , tốc độ ban đầu của vật là 4 m/s. Sau khi đi qd S tốc độ của vật đạt 12 m/s. Tính tốc độ trung bình của vật trong qd nói trên, biết chuyển động của vật trong mỗi giây là đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2023
Phương trình chuyển động của vật: \(x=t^2+4t+20\)
\(\left\{{}\begin{matrix}x_0=20m\\v_0=4m/s\\a=2m/s^2\end{matrix}\right.\)
Phương trình quãng đường vật chuyển động: \(S=4t+t^2\)
Tốc độ trung bình của vật chuyển động trong 4s đầu là:
\(v_{tb}=\dfrac{S}{t}=\dfrac{32}{4}=8\left(m/s\right)\)
VT
22 tháng 9 2017
Đáp án C
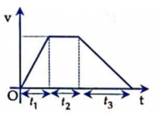
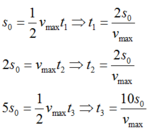
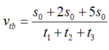
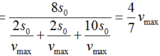
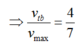
Chú ý: Vật chuyển động gồm ba giai đoạn (như hình vẽ): nhanh dần – đều – chậm dần đều ta có công thức
21 tháng 6 2016
gọi quãng đường đi là 2s
thời gian đi nửa đoạn đầu : t1=\(\frac{s}{40}\) (h)
thời gian đi nửa đoạn sau: \(t_2=\frac{s}{30}\) (h)
=> vận tốc trung bình :\(v_{tb}=\frac{2s}{t_1+t_2}=\frac{2s}{\frac{s}{40}+\frac{s}{30}}=\frac{2s}{\frac{7s}{120}}\approx34,29\)km/h
4 tháng 10 2023
Tóm tắt:
t1=2h; \(v_1\)=30km/h
t2=3h;\(v_2\)=50km/h
t3=1h;\(v_3\)=60km/h
t4=2h;\(v_4\)=20km/h
Giải:
Tốc độ trung bình trên cả quãng đường đi là:
\(v\)=\(\dfrac{s}{t}\)\(=\dfrac{s_1+s_2+s_3+s_4}{t_1+t_2+t_3+t_4}\)
\(=\dfrac{v_1.t_1+v_2.t_2+v_3.t_3+v_4.t_4}{t_1+t_2+t_3+t_4}\)\(=\dfrac{30.2+50.3+60.1+20.2}{2+3+1+2}=38,75km\)/h
