( 3x - 21 ) . (43 - x ) =o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NC
1
21 tháng 7 2019
a) \(\left(3x-1\right)^2-\left(x+3\right)^2=0\)
\(=>\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(=>\left(4x+2\right)\left(2x-4\right)=0\)
\(=>4\left(2x+1\right)\left(x-2\right)=0\)
\(=>\orbr{\begin{cases}2x+1=0\\x-2=0\end{cases}}\)
\(=>\orbr{\begin{cases}x=-\frac{1}{2}\\x=2\end{cases}}\)
b)\(x^3-\frac{x}{49}=0=>x\left(x^2-\frac{1}{49}\right)=0=>x\left(x-\frac{1}{7}\right)\left(x+\frac{1}{7}\right)=0\)
\(=>x=0\)hoặc \(x=\frac{1}{7}\) hoặc \(x=-\frac{1}{7}\)
21 tháng 7 2019
a)\(\(\left(3x-1\right)^2-\left(x+3\right)^2=0\)\)
\(\(\Leftrightarrow\left(3x-1-x-3\right)\left(3x-1+x+3\right)=0\)\)
\(\(\Leftrightarrow\left(2x-4\right)\left(4x+2\right)=0\)\)
\(\(\Leftrightarrow\orbr{\begin{cases}2x-4=0\\4x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-\frac{1}{2}\end{cases}}}\)\)
b)\(\(x^3-\frac{x}{49}=0\)\)
\(\(\Leftrightarrow\frac{49x^3-x}{49}=0\)\)
\(\(\Leftrightarrow x\left(49x^2-1\right)=0\)\)
\(\(\Leftrightarrow\orbr{\begin{cases}x=0\\49x^2-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=0\\\left(7x-1\right)\left(7x+1\right)=0\end{cases}}}\)\)\
\(\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{7};x=-\frac{1}{7}\end{cases}}\)\)
c)\(\(x^2-7x+12=0\)\)
\(\(\Leftrightarrow\left(x-4\right)\left(x-3\right)=0\)\)
\(\(\Leftrightarrow\orbr{\begin{cases}x-4=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=4\\x=3\end{cases}}}\)\)
d) \(\(4x^2-3x-1=0\)\)
\(\(\Leftrightarrow4x^2-4x+x-1=0\)\)
\(\(\Leftrightarrow4x\left(x-1\right)+\left(x-1\right)=0\)\)
\(\(\Leftrightarrow\left(x-1\right)\left(4x+1\right)=0\)\)
\(\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\4x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{1}{4}\end{cases}}}\)\)
e) Tham khảo tại : [Toán 8]Giải phương trình | Cộng đồng học sinh Việt Nam - HOCMAI Forum
https://diendan.hocmai.vn/threads/toan-8-giai-phuong-trinh.290061/
_Y nguyệt_
NM
1
PT
1
CM
15 tháng 2 2019
Ta thấy:
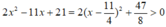
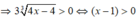
Áp dụng bất đẳng thức Cô – si ta có:
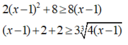
Cộng vế với vế ta được:
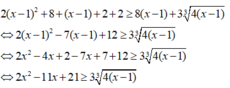
Dấu “=” xảy ra khi và chỉ khi x - 1 = 2 ⇔ x = 3
Vậy x = 3 là nghiệm của phương trình.
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
c.
ĐKXĐ: \(\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\)
\(\Leftrightarrow x+4-2\sqrt[]{\left(\dfrac{x+2}{x-1}\right)^2\left(\dfrac{x-1}{x+2}\right)}=0\)
\(\Leftrightarrow x+4-2\sqrt[]{\dfrac{x+2}{x-1}}=0\)
\(\Leftrightarrow x+4=2\sqrt[]{\dfrac{x+2}{x-1}}\) (\(x\ge-4\))
\(\Leftrightarrow x^2+8x+16=\dfrac{4\left(x+2\right)}{x-1}\)
\(\Rightarrow x^3+7x^2+4x-24=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2+4x-8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2+2\sqrt{3}\\x=-2-2\sqrt{3}\left(loại\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 7 2021
a.
\(\Leftrightarrow2x^2-11x+21=3\sqrt[3]{4\left(x-1\right)}\)
Do \(2x^2-11x+21=2\left(x-\dfrac{11}{4}\right)^2+\dfrac{47}{8}>0\Rightarrow3\sqrt[3]{4\left(x-1\right)}>0\Rightarrow x-1>0\)
Ta có:
\(VT=2x^2-11x+21-3\sqrt[3]{4x-4}=2\left(x^2-6x+9\right)+x+3-3\sqrt[3]{4\left(x-1\right)}\)
\(=2\left(x-3\right)^2+x+3-3\sqrt[3]{4\left(x-1\right)}\)
\(\Rightarrow VT\ge x+3-3\sqrt[3]{4\left(x-1\right)}=\left(x-1\right)+2+2-3\sqrt[3]{4\left(x-1\right)}\)
\(\Rightarrow VT\ge3\sqrt[3]{\left(x-1\right).2.2}-3\sqrt[3]{4\left(x-1\right)}=0\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left(x-3\right)^2=0\\x-1=2\\\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy pt có nghiệm duy nhất \(x=3\)
4 tháng 3 2022
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
4 tháng 3 2022
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
DN
x3 + 3x2 - 25x + 21 = 0
Dạng giải phương trình, mấy thánh giỏi rõ giùm em, đừng ghi tắt nha... Hậu tạ
1
9 tháng 8 2017
Cái này nhẩm nghiệm được mà,do tổng các hệ số =0 >>>Pt có 1 nghiệm là 1>>>có chứa nhân tử x-1.
Phân tích:x^3+3x^2-25x+21=x^3-x^2+4x^2-4x-21x+21
=(x^2+4x-21)(x-1)=(x+7)(x-3)(x-1)>>>phương trình có 3 nghiệm là -7,3,1
18 tháng 5 2021
3(2x+y)-2(3x-2y)=3.19-11.2
6x+3y-6x+4y=57-22
7y=35
y=5
thay vào :
2x+y=19
2x+5=19
2x=14
x=7
2/ x2+21x-1x-21=0
x(x+21)-1(x+21)=0
(x+21)(x-1)=0
TH1 x+21=0
x=-21
TH2 x-1=0
x=1
vậy x = {-21} ; {1}
3/ x4-16x2-4x2+64=0
x2(x2-16)-4(x2-16)=0
(x2-16)-(x2-4)=0
TH1 x2-16=0
x2=16
<=>x=4;-4
TH2 x2-4=0
x2=4
x=2;-2
18 tháng 5 2021
Bài 1 :
\(\hept{\begin{cases}2x+y=19\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}4x+2y=38\\3x-2y=11\end{cases}\Leftrightarrow\hept{\begin{cases}7x=49\\2x+y=19\end{cases}}}}\)
\(\Leftrightarrow\hept{\begin{cases}x=7\\2x+y=19\end{cases}}\)Thay vào x = 7 vào pt 2 ta được :
\(14+y=19\Leftrightarrow y=5\)Vậy hệ pt có một nghiệm ( x ; y ) = ( 7 ; 5 )
Bài 2 :
\(x^2+20x-21=0\)
\(\Delta=400-4\left(-21\right)=400+84=484\)
\(x_1=\frac{-20-22}{2}=-24;x_2=\frac{-20+22}{2}=1\)
Bài 3 : Đặt \(x^2=t\left(t\ge0\right)\)
\(t^2-20t+64=0\)
\(\Delta=400+4.64=656\)
\(t_1=\frac{20+4\sqrt{41}}{2}\left(tm\right);t_2=\frac{20-4\sqrt{41}}{2}\left(ktm\right)\)
Theo cách đặt : \(x^2=\frac{20+4\sqrt{41}}{2}\Rightarrow x=\sqrt{\frac{20+4\sqrt{41}}{2}}=\frac{\sqrt{20\sqrt{2}+4\sqrt{82}}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-21=0\\43-x=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=7\\x=43\end{matrix}\right.\)
Vậy x = 7 hoặc x = 43
\(\left(3x-21\right)\cdot\left(43-x\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x-21=0\\43-x=0\end{matrix}\right.\\\Rightarrow\left[{}\begin{matrix}x=7\\x=43\end{matrix}\right. \)
Vậy: \(x=7;x=43\)