9/4-1/4:y-1/2=2/3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
\(\overrightarrow{AB}=\left(1;2\right)\Rightarrow\) đường thẳng AB nhận (2;-1) là 1 vtpt
Phương trình AB:
\(2\left(x-1\right)-1\left(y+3\right)=0\Leftrightarrow2x-y-5=0\)
b.
d vuông góc \(\Delta\Rightarrow d\) nhận (4;-3) là 1 vtpt
Phương trình d có dạng: \(4x-3y+c=0\)
\(d\left(B;d\right)=\dfrac{\left|4.2-3.\left(-1\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{2}{5}\)
\(\Leftrightarrow\left|c+11\right|=2\Rightarrow\left[{}\begin{matrix}c=-9\\c=-13\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}4x-3y-13=0\\4x-3y-9=0\end{matrix}\right.\)

a: \(\left\{{}\begin{matrix}x+4y=-11\\5x-4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x=-10\\x+4y=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{-5}{3}\\y=\dfrac{-11-x}{4}=\dfrac{-11+\dfrac{5}{3}}{4}=-\dfrac{7}{3}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}2x-y=7\\3x+5y=-22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-3y=21\\6x+15y=-66\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-18y=78\\2x-y=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-13}{3}\\x=\dfrac{y+7}{2}=\dfrac{4}{3}\end{matrix}\right.\)

1. \(\left\{{}\begin{matrix}3x+4y=11\\2x-y=-11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+4y=11\\8x-4y=-44\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x+4y=11\\11x=-33\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=-3\end{matrix}\right.\)
2. \(\left\{{}\begin{matrix}3x+2y=0\\2x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=0\\4x+2y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=-2\end{matrix}\right.\)
3.\(\left\{{}\begin{matrix}3x+\dfrac{5}{2}y=9\\2x+\dfrac{1}{3}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+5y=18\\6x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4y=12\\6x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3\\x=\dfrac{1}{2}\end{matrix}\right.\)

Đáp án D
Mặt phẳng cần tìm sẽ vuông góc với (ABM). Một vecto pháp tuyến của nó là tích có hướng của vecto pháp tuyến mặt phẳng (ABM) và A B →
Cũng có thể làm như sau: Khoảng cách lớn nhất là MH với H là hình chiếu vuông góc của M lên đường thẳng AB. Ta tìm được H(3;-3;-10)

Đáp án D
Mặt phẳng cần tìm sẽ vuông góc với (ABM). Một vecto pháp tuyến của nó là tích có hướng của vecto pháp tuyến mặt phẳng (ABM) và A B →
Cũng có thể làm như sau: Khoảng cách lớn nhất là MH với H là hình chiếu vuông góc của M lên đường thẳng AB. Ta tìm được H ( 3 ; − 3 ; − 10 ) .

ĐKXĐ: ...
\(y\left(y^2-5y+4\right)+y^2=\left(y^2-5y+4\right)\sqrt{x+1}+x+1\)
\(\Leftrightarrow\left(y^2-5y+4\right)\left(y-\sqrt{x+1}\right)+\left(y+\sqrt{x+1}\right)\left(y-\sqrt{x+1}\right)=0\)
\(\Leftrightarrow\left(y-\sqrt{x+1}\right)\left[\left(y-2\right)^2+\sqrt{x+1}\right]=0\)
\(\Leftrightarrow y=\sqrt{x+1}\Rightarrow y^2=x+1\)
Thế xuống pt dưới:
\(2\sqrt{x^2-3x+3}+6x-7=\left(x+1\right)\left(x-1\right)^2+x\sqrt{3x-2}\)
\(\Leftrightarrow2\left(\sqrt{x^2-3x+3}-1\right)+x\left(x-\sqrt{3x-2}\right)=x^3-7x+6\)
\(\Leftrightarrow\dfrac{2\left(x^2-3x+2\right)}{\sqrt{x^2-3x+3}+1}+\dfrac{x\left(x^2-3x+2\right)}{x+\sqrt{3x-2}}=\left(x+3\right)\left(x^2-3x+2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x+2=0\\\dfrac{2}{\sqrt{x^2-3x+3}+1}+\dfrac{x}{x+\sqrt{3x-2}}=x+3\left(1\right)\end{matrix}\right.\)
Xét (1) với \(x\ge\dfrac{3}{2}\):
\(\dfrac{2}{\sqrt{x^2-3x+3}+1}\le8-4\sqrt{3}< 1\)
\(\sqrt{3x-2}\ge0\Rightarrow\dfrac{x}{x+\sqrt{3x-2}}\le1\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{2}{\sqrt{x^2-3x+3}+1}+\dfrac{x}{x+\sqrt{3x-2}}< 2\\x+3>2\end{matrix}\right.\)
\(\Rightarrow\left(1\right)\) vô nghiệm

ĐK: \(x,y\ne-1\)
hpt \(\Leftrightarrow\)\(\hept{\begin{cases}\frac{x^2}{y^2+2y+1}+\frac{y^2}{x^2+2x+1}=\frac{8}{9}\\\frac{4x+4y-5xy+4}{xy+x+y+1}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}\frac{x^2}{\left(y+1\right)^2}+\frac{y^2}{\left(x+1\right)^2}=\frac{8}{9}\\4-\frac{9xy}{\left(x+1\right)\left(y+1\right)}\end{cases}}\)
\(\Leftrightarrow\)\(\hept{\begin{cases}a^2+b^2=\frac{8}{9}\\ab=\frac{4}{9}\end{cases}}\)\(\left(a;b\right)=\left(\frac{x}{y+1};\frac{y}{x+1}\right)\)

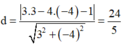
\(\dfrac{9}{4}-\dfrac{1}{4}:y-\dfrac{1}{2}=\dfrac{2}{3}\\ =>\dfrac{1}{4}:y=\dfrac{9}{4}-\dfrac{1}{2}-\dfrac{2}{3}\\ =>\dfrac{1}{4}:y=\dfrac{27}{12}-\dfrac{6}{12}-\dfrac{8}{12}\\ =>\dfrac{1}{4}:y=\dfrac{13}{12}\\ =>y=\dfrac{1}{4}:\dfrac{13}{12}\\ =>y=\dfrac{3}{13}\)
`9/4- 1/4:y - 1/2 = 2/3`
`<=> 9/4 - 1/4:y - 2/4 = 2/3`
`<=> 7/4 - 1/4:y= 2/3`
`<=> 1/4:y = 7/4 - 2/3`
`<=> 1/4:y = 21/12 - 8/12`
`<=> 1/4:y = 13/12`
`<=> y = 1/4 : 13/12`
`<=> y = 1/4 . 12/13`
`<=> y = 3/13`
Vậy ..