A=(x+1)+(x+5/45)+(x+5/117)+(x+221)=10
Giúp mình với mình can gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 8 2019
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
CM
14 tháng 9 2018
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
2.1
a.
\(\Leftrightarrow sinx-cosx=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{4}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5\pi}{12}+k2\pi\\x=\dfrac{13\pi}{12}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
b.
\(cosx-\sqrt{3}sinx=1\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{3}=\dfrac{\pi}{3}+k2\pi\\x+\dfrac{\pi}{3}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
PT
1
CM
20 tháng 1 2018
Ta có: ax + by = c ⇔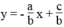
Để phương trình ax + by = c xác định một hàm số bậc nhất của biến x thì a ≠ 0 và b ≠ 0.
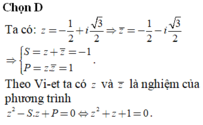
\(A=\left(x+1\right)+\left(x+\dfrac{5}{45}\right)+\left(x+\dfrac{5}{117}\right)+\left(x+221\right)=10\\ \Rightarrow x+1+x+\dfrac{1}{9}+x+\dfrac{5}{117}+x+221=10\\ \Rightarrow4x+\left(1+\dfrac{1}{9}+\dfrac{5}{117}+221\right)=10\\ \Rightarrow4x+\dfrac{2888}{13}=10\\ \Rightarrow4x=10-\dfrac{2888}{13}\\ \Rightarrow4x=-\dfrac{2758}{13}\\ \Rightarrow x=-\dfrac{1379}{26}\)
Cho hỏi 1/9 ở đâu v ak