cho tam giác ABC vuông tại A. Chứng minh các đẳng thức sau:
a. tan 𝐴 = sin A / cos 𝐴
b. sin2 𝐴 + cos2 𝐴 = 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 4 2015
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
SC
27 tháng 3 2016
a) Xét tam giác vuông AHC có AC là cạnh lớn nhất ( cạnh lớn nhất trong tam giác vuông) => AC>HC (1) Xét tam giác vuông AHB có AB là cạnh lớn nhất (canh lớn nhất trong tam giác vuông) =>AB>HB (2) Ta có : HC+HB+BC ( H nằm giũa A và C) (3) Từ (1) , (2) và (3) => AC+AB>BC b)Xét tam giác ABC có BC là cạnh lớn nhất(gt) =>BC>AB Ta có : AC>0 => BC+AC>AB Xét tam giác ABC có BC là cạnh lớn nhất (gt) =>BC>AC Vì AB>0=>BC+AB>AC
CM
15 tháng 12 2018
Theo giả thiết, tam giác ABC có độ dài cạnh BC là lớn nhất nên chân đường vuông góc kẻ từ A đến cạnh BC chắn chắn phải nằm giữa B và C.
Suy ra H nằm giữa B và C.
⇒ HB + HC = BC
+) Xét tam giác AHB vuông tại H ta có: HB < AB (1) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
+) Xét tam giác AHC vuông tại H ta có: HC < AC (2) (vì trong tam giác vuông cạnh huyền là cạnh lớn nhất)
Lấy (1) + (2) ta được:
HB + HC < AB + AC
Mà HB + HC = BC suy ra BC < AB + AC hay AB + AC > BC
19 tháng 4 2017
a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)
CM
5 tháng 9 2017
Xét tam giác ABC vì BC là cạnh lớn nhất nên AB < BC và AC < BC.
Mà ta lại có: AC > 0 và AB > 0 hay 0 < AC và 0 < AB
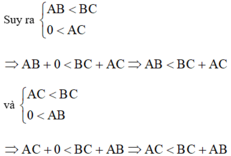
⇒ Đpcm
LN
0
16 tháng 8 2021
a, xét tam giác CHA và tg CHO có : CH chung
AH = HO do H là trđ của AO (gt)
^CHA = ^CHO = 90
=> tg CHA = tg CHO (2cgv)
=> CH = CO
có AB _|_ CD => A là điểm chính giữa của cung CD => AC = AD mà OC = OD
=> AC = CO = OD = DA
=> ACOD là hình thoi
b, C thuộc đường tròn đường kính AB => ^ACB = 90 => AC _|_ CB
có AC // DO do ACOD là hình thoi
=> DO _|_ CB
M là trung điểm của dây BC (Gt) => OM _|_ BC (định lí)
=> D;O;M thẳng hàng
c, xét tg ACB có ^ACB = 90 và CH _|_ AB
=> AH.HB = CH^2
=> 4AH.HB = 4CH^2
=> 4AH.HB = (2CH)^2
mà 2CH = CD
=> CD^2 = 4AH.HB