bt lớp 7 vẽgóc xoy=70 độ vẽ góc yoz kề bù với góc xoy vẽ tia om là tia phân giác của góc xoyvẽ tia on là tia phân giác của xoz tính gó xon
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 7 2017
Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi
LL
giúp mình câu 4,6,14 ( sách bài tập toán 7-tập 1) phần hình học chương 1
1
HN
21 tháng 6 2017
Bài 6:
a) \(\widehat{MAP}=\widehat{NAQ}\) (hai góc đối đỉnh)
Mà \(\widehat{MAP}=33^o\)
Vậy \(\widehat{NAQ}=33^o\).
b) Ta có: \(\widehat{MAP}+\widehat{MAQ}=180^o\) (hai góc kề bù)
Mà \(\widehat{MAP}=33^o\)
Nên \(\widehat{MAQ}=180^o-\widehat{MAP}=180^o-33^o=147^o\)
Vậy \(\widehat{MAQ}=147^o.\)
c) Các cặp góc đối đỉnh:
\(\widehat{MAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAP}\) và \(\widehat{MAQ}\).
d) Các cặp góc bù nhau:
\(\widehat{MAP}\) và \(\widehat{NAP}\)
\(\widehat{NAP}\) và \(\widehat{NAQ}\)
\(\widehat{NAQ}\) và \(\widehat{MAQ}\)
\(\widehat{MAQ}\) và \(\widehat{MAP}\).
13 tháng 1 2019
chưa chị nhưng em đã biết rồi nên chị mà biết thì chỉ cho e
9 tháng 2 2017
*Nhìn vào hình vẽ ta thấy QAM và QAN là 2 góc kề bù
=>AQ nằm giữa AM và AN
=>QAM+QAN=MAN
Thay MAN=1800 ; QAN=580
=>QAM+580=1800
=>QAM=1800-580=1220
*Ta có: AP, AQ cùng nằm trên 1 nửa mặt phẳng bờ chứa đoạn thẳng MN (1)
Ma PAM=330; QAM=1220 =>PAM<QAM(2)
Từ (1) và (2) => AP nằm giữa 2 đoạn thẳng AM va AQ
=>QAP+PAM=QAM
Thay QAM=1220; PAM=330
=>QAP+330=1220
=>QAP=1220-330=890
Vay QAP=890
Ủng hộ mk bạn nhé
NN
9 tháng 2 2017
số đo x là : 180-33-58= 89 ( độ )
mk có sách này vì mk đnag học lớp 6
T
18 tháng 4 2019
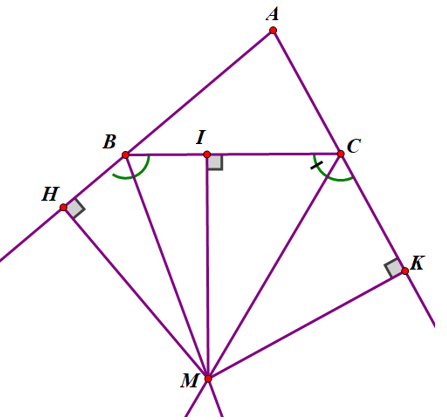
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
On là phân giác của góc xOz
=>\(\widehat{xOn}=\dfrac{\widehat{xOz}}{2}=\dfrac{180^0}{2}=90^0\)