\(\dfrac{x}{3}\) = \(\dfrac{y}{4}\) = \(\dfrac{z}{5}\) và 2x2 + 2y2 + 3z2 = -100
2x = \(\dfrac{y}{3}\) = \(\dfrac{z}{5}\) và x + y - \(\dfrac{z}{2}\) = -20
\(\dfrac{15}{x-9}\) = \(\dfrac{20}{y-12}\) \(\dfrac{40}{z-24}\) và xy = 1200
\(\dfrac{40}{x-30}\) = \(\dfrac{28}{y-15}\) = \(\dfrac{28}{z-21}\) và xyz = 22400
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Đa thức bậc nhất có hệ số của biến bằng – 2 và hệ số tự do bằng 6 tức \(a = - 2;b = 6\)
\( - 2x + 6\).
b) Đa thức bậc hai có hệ số tự do bằng 4: \({x^2} + x + 4\).
c) Đa thức bậc bốn có hệ số của lũy thừa bậc 3 của biến bằng 0: \({x^4} + 0.{x^3} + {x^2} + 1 = {x^4} + {x^2} + 1\).
d) Đa thức bậc sáu trong đó tất cả hệ số của lũy thừa bậc lẻ của biến đều bằng 0: \({x^6} + 0.{x^5} + {x^4} + 0.{x^3} + {x^2} + 0.x = {x^6} + {x^4} + {x^2}\).

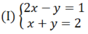
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
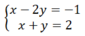
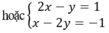

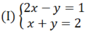
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
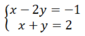
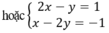

a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c) 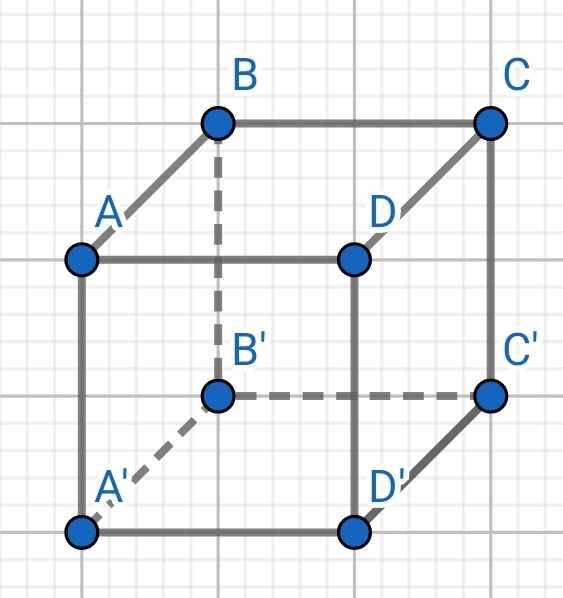
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3

ta có P(x) = (x-1)(x-2)(x-3) + R(x) ( R(x) = mx^2 + nx + i)
=> P(1) = m . 1 + n.1 + i = -15
=> P(2) = m . 2^2 + n . 2 + i = -15
=> P(3) = m . 3^2 + n . 3 + i = -9
còn lại tự làm nhé

a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.

Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.

Gọi A là đa thức cần tìm
Đa thức bậc năm một biến có hai hạng tử mà hệ số cao nhất là 2 nên Đa thức chắc chắn sẽ có dạng là \(A=2x^5+B\)
Hệ số tự do là 64 mà đa thức A chỉ có hai hạng tử nên \(A=2x^5+64\)
Đặt A=0
=>\(2x^5+64=0\)
=>\(x^5+32=0\)
=>\(x^5=-32\)
=>x=-2

\(x^2+2\left(2m-1\right)x+3\left(m^2-1\right)=0\)
\(a,\) Để pt có nghiệm thì \(\Delta\ge0\)
\(\Rightarrow\left[2\left(2m-1\right)\right]^2-4\left[3\left(m^2-1\right)\right]\ge0\)
\(\Rightarrow4\left(4m^2-4m+1\right)-4\left(3m^2-3\right)\ge0\)
\(\Rightarrow16m^2-16m+4-12m^2+12\ge0\)
\(\Rightarrow4m^2-16m+16\ge0\)
\(\Rightarrow\left(2m-4\right)^2\ge0\)
Vậy pt có nghiệm với mọi m.
b, Theo viét : \(\left\{{}\begin{matrix}x_1+x_2=-2\left(2m-1\right)\\x_1x_2=3\left(m^2-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=-4m+2\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{-2+x_1+x_2}{4}\\x_1x_2=3\left(\dfrac{-2+x_1+x_2}{4}\right)^2-3\end{matrix}\right.\)
Vậy......
a: Đặt \(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=k\)
=>x=3k; y=4k; z=5k
\(2x^2+2y^2+3z^2=-100\)
=>\(2\left(3k\right)^2+2\cdot\left(4k\right)^2+3\cdot\left(5k\right)^2=-100\)
=>\(125k^2=-100\)
=>\(k^2=-\dfrac{4}{5}\)(vô lý)
vậy: \(\left(x;y;z\right)\in\varnothing\)
b: 2x=y/3=z/5
=>\(\dfrac{x}{\dfrac{1}{2}}=\dfrac{y}{3}=\dfrac{z}{5}=k\)
=>\(x=\dfrac{1}{2}k;y=3k;z=5k\)
\(x+y-\dfrac{z}{2}=-20\)
=>\(\dfrac{1}{2}k+3k-\dfrac{5k}{2}=-20\)
=>k=-20
=>\(x=\dfrac{1}{2}\cdot\left(-20\right)=-10;y=3\cdot\left(-20\right)=-60;z=5\cdot\left(-20\right)=-100\)