Cho tam giác ABC có \(\widehat{A}=2\widehat{B}=3\widehat{C}=4\alpha\)CM \(\frac{1}{AB}=\frac{1}{AC}+\frac{1}{BC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

20 tháng 7 2020
Mình đã làm rùi và rất ngại làm lại nên bạn chịu khó nhìn nha ! Vào TKHĐ của mình

HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
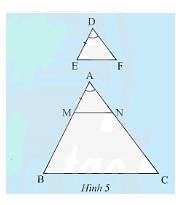
a) Vì \(MN//BC\left( {M \in AB,N \in AC} \right)\) nên \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\)(định lí Thales).
b) Vì \(AM = DE\) mà \(\frac{{DE}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AM}}{{AB}} = \frac{1}{3} \Rightarrow \frac{{AN}}{{AC}} = \frac{1}{3} \Rightarrow AN = \frac{1}{3}AC\).
Lại có \(DF = \frac{1}{3}AC\) nên \(AN = DF = \frac{1}{3}AC\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
d) Dự đoán hai tam giác \(DEF\) và \(ABC\) đồng dạng.