Cho \(\Delta ABC\)có\(AB=3,14cm\) ,\(AC=5,37cm\)và \(\widehat{B}-\widehat{C}=90^0.\)Tính độ dài đương cao \(AH\)(lấy kết quả 4 chữ số thập phân).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 7 2023
a: AB=BC*cos60=6*1/2=3cm
AC=căn 6^2-3^2=3*căn 3\(\simeq5.2\left(cm\right)\)
b: HB=AB^2/BC=1,5cm
HC=6-1,5=4,5cm
24 tháng 7 2023
c) Tam giác BCD, có: BC=BD=> Tam giác BCD cân tại B=>BDC=BCD
Mặt khác: BDC+BCD=ABC=60 độ (tính chất góc ngoài của tam giác)
=>BDC=BCD=30 độ
Tam giác ABC vuông tại A, có: ABC+ACB=90 độ
=>ACB=90 độ-ABC=90 độ-60 độ=30 độ
=>ACD= DCB+BCA=30 độ+30 độ= 60 độ
Xét 2 tam giác ABC và ACD,có:
ABC=ACD=60 độ
ACB=ADC=30 độ
=> tam giác ABC đồng dạng tam giác ACD (g-g)
=>\(\dfrac{AB}{BC}=\dfrac{AC}{CD}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\) (vì BD=BC)
15 tháng 7 2017
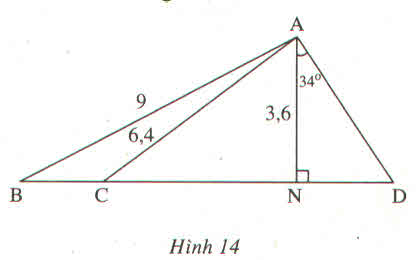
a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)
B
22 tháng 9 2017
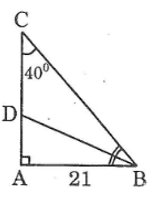
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)
23 tháng 12 2017
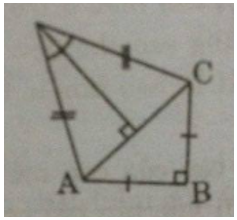
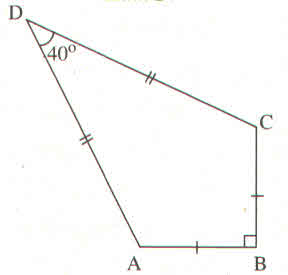
a) Nối AC và kẻ DH⊥ACDH⊥AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2=AB2+BC2=122+122=144+144=288AC2=AB2+BC2=122+122=144+144=288
Suy ra: AC=12√2(cm)AC=122(cm)
Ta có: tam giác ACD cân tại D
DH⊥ACDH⊥AC
Suy ra: HA=HC=AC2=6√2(cm)HA=HC=AC2=62(cm)
ˆADH=12ˆADC=20∘ADH^=12ADC^=20∘
Trong tam giác vuông ADH, ta có:
AD=AHsinˆADH=6√2sin20∘≈24,809(cm)AD=AHsinADH^=62sin20∘≈24,809(cm)
b) Ta có:
SABC=12.AB.BC=12.12.12=72SABC=12.AB.BC=12.12.12=72 (cm2)
Trong tam giác vuông ADH, ta có:
DH=AH.cotgˆADH=6√2.cotg20∘≈23,313(cm)DH=AH.cotgADH^=62.cotg20∘≈23,313(cm)
Mặt khác:
SADC=12.DH.AC≈12.23,313.12√2=197,817SADC=12.DH.AC≈12.23,313.122=197,817 (cm2)
Vậy Sdiều =SABC+SADC=72+197,817=269,817=SABC+SADC=72+197,817=269,817 (cm2)
23 tháng 12 2017
a, nối AC rồi kẻ
Áp dụng định lý Pi-ta-go vào tam giác vuông ABC:
Suy ra:
ta có:tam giác ABC cân tại D
Suy ra:
Trong tam giác vuông ADH, ta có
b, Ta có:
(cm2)
Trong tam giác vuông ADH, ta có:
Mặt khác
(cm2)
Vậy S (cm2)
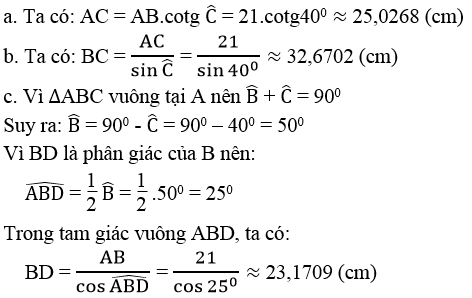
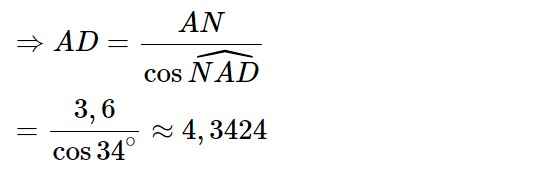
Vì \(\widehat{ABC}-\widehat{C}=90^O\) nên góc B là góc tù. Ta có: \(180^o-\widehat{ABH}-\widehat{C}=90^O\Rightarrow\widehat{ABH}+\widehat{C}=90^O\)=> 2 góc phụ nhau\(\Rightarrow sin\widehat{ABH}=cosC\)
\(sin\widehat{ABH}=\frac{AH}{3,14}\Rightarrow cos^2\widehat{C}=\frac{AH^2}{3,14^2}\)
\(sinC=\frac{AH}{5,37}\Rightarrow sin^2C=\frac{AH^2}{5,37^2}\)
\(\Rightarrow cos^2C+sin^2C=AH^2\left(\frac{1}{3,14^2}+\frac{1}{5,37^2}\right)\)
\(\Rightarrow1=AH^2\left(\frac{1}{3,14^2}+\frac{1}{5,37^2}\right)\Rightarrow AH\approx2,7106\)
Độ dài đường cao AH là: 2,7106 cm
Bạn anhduc1501 trình bày cách làm rồi
Bạn xem đi nha!
Chúc bạn học tốt!