phan tich da thuc sau thanh nhan tu
a (x^2 +5x+6)(x^2-15x+56)-144
b (X^2-11x+28)(x^2-7x+10)-72
giai ho to vs ,to dang can gap
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 11 2018
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
4 tháng 6 2017
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: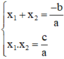 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
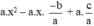
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm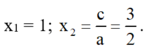 
Vậy: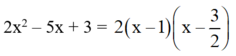 
CM
30 tháng 8 2017
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
23 tháng 7 2017
Phương trình 5 x 2 + 21x − 36 = 0 có a + b + c = 5 +21 – 26 = 0 nên phương trình có hai nghiệm phân biệt là x 1 = 1 ; x 2 = - 26 5 . Khi đó B = 5. (x − 1) x + 26 5
Đáp án: C
CM
17 tháng 5 2018
Phương trình 18 x 2 + 23x + 5 = 0 có a – b + c = 18 – 23 + 5 = 0 nên phương trình có hai nghiệm phân biệt là x 1 = − 1 ; x 2 = − 5 18 . Khi đó A = 18 (x + 1) x + 5 18
Đáp án: A
H9
HT.Phong (9A5)
CTVHS
10 tháng 8 2023
Bài 2:
1) \(x^2-4x+4=\left(x-2\right)^2\)
2) \(x^2-9=x^2-3^2=\left(x-3\right)\left(x+3\right)\)
3) \(1-8x^3=\left(1-2x\right)\left(1+2x+4x^2\right)\)
4) \(\left(x-y\right)^2-9x^2=\left(x-y\right)^2-\left(3x\right)^2=\left(x-y-3x\right)\left(x-y+3x\right)=\left(-2x-y\right)\left(4x-y\right)\)
5) \(\dfrac{1}{25}x^2-64y^2=\left(\dfrac{1}{5}x-8y\right)\left(\dfrac{1}{5}x+8y\right)\)
6) \(8x^3-\dfrac{1}{8}=\left(2x-\dfrac{1}{2}\right)\left(4x^2+x+\dfrac{1}{4}\right)\)
DT
9
LN
30 tháng 10 2017
ak
x8 + -7x4 + -8 = 0 Reorder the terms: -8 + -7x4 + x8 = 0 Solving -8 + -7x4 + x8 = 0 Solving for variable 'x'. Factor a trinomial. (-1 + -1x4)(8 + -1x4) = 0
G
10 tháng 8 2023
\(4a^2b^2-\left(a^2+b^2-c^2\right)^2\)
\(=4a^2b^2-2ab\left(a^2+b^2-c^2\right)+2ab\left(a^2+b^2-c^2\right)-\left(a^2+b^2-c^2\right)^2\)
\(=2ab\left[2ab-\left(a^2+b^2-c^2\right)\right]+\left(a^2+b^2-c^2\right)\left[2ab-\left(a^2+b^2-c^2\right)\right]\)
\(=\left(2ab+a^2+b^2-c^2\right)\left(2ab-a^2-b^2+c^2\right)\)
\(=\left(a^2+ab+ab+b^2-c^2\right)\left[c^2-\left(a^2-ab-ab+b^2\right)\right]\)
\(=\left[a\left(a+b\right)+b\left(a+b\right)-c^2\right]\left[c^2-\left(a\left(a-b\right)-b\left(a-b\right)\right)\right]\)
\(=\left[\left(a+b\right)^2-c^2\right]\left[c^2-\left(a-b\right)^2\right]\)
\(=\left[\left(a+b\right)^2-c\left(a+b\right)+c\left(a+b\right)-c^2\right]\left[c^2+c\left(a-b\right)-c\left(a-b\right)-\left(a-b\right)^2\right]\)
\(=\left[\left(a+b\right)\left(a+b-c\right)+c\left(a+b-c\right)\right]\left[c\left(c+a-b\right)-\left(a-b\right)\left(c+a-b\right)\right]\)
\(=\left(a+b+c\right)\left(a+b-c\right)\left(c+a-b\right)\left(c-a+b\right)\)
\(a.\left(x^2+5x+6\right)\left(x^2-15x+56\right)-144\\ =\left(x+2\right)\left(x+3\right)\left(x-7\right)\left(x-8\right)-144\\ =\left[\left(x+2\right)\left(x-7\right)\right]\left[\left(x+3\right)\left(x-8\right)\right]-144\\ =\left(x^2-5x-14\right)\left(x^2-5x-24\right)-144\\ =\left(x^2-5x-19+5\right)\left(x^2-5x-19-5\right)-144\\ =\left(x^2-5x-19\right)^2-5^2-144\\ =\left(x^2-5x-19\right)^2-169\\ =\left(x^2-5x+19\right)^2-13^2\\ =\left(x^2-5x-19-13\right)\left(x^2-5x-19+13\right)\\ =\left(x^2-5x-32\right)\left(x^2-5x-6\right)\\ =\left(x^2-5x-32\right)\left(x+1\right)\left(x-6\right)\)
\(b.\left(x^2-11x+28\right)\left(x^2-7x+10\right)-72\\ =\left(x-4\right)\left(x-7\right)\left(x-5\right)\left(x-2\right)-72\\ =\left[\left(x-4\right)\left(x-5\right)\right]\left[\left(x-7\right)\left(x-2\right)\right]-72\\ =\left(x^2-9x+20\right)\left(x^2-9x+14\right)-72\\ =\left(x^2-9x+17+3\right)\left(x^2-9x+17-3\right)-72\\ =\left(x^2-9x+17\right)^2-3^2-72\\ =\left(x^2-9x+17\right)^2-81\\ =\left(x^2-9x+17\right)^2-9^2\\ =\left(x^2-9x+17-9\right)\left(x^2-9x+17+9\right)\\ =\left(x^2-9x+8\right)\left(x^2-9x+26\right)\\ =\left(x-1\right)\left(x-8\right)\left(x^2-9x+26\right)\)