Cho A =2x^3 ; B =-3x^4 . Biết đơn thức A và B cùng dấu. So sánh x với 0
Giúp ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
22 tháng 10 2017
Với a, b ∈ Z; b ≠ 0 thì:
- Khi a, b cùng dấu thì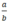 
> 0
- Khi a, b khác dấu thì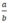 
< 0
Tổng quát: Số hữu tỉ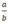 
(a, b ∈ Z; b ≠ 0) > 0 nếu a, b cùng dấu; < 0 nếu a, b khác dấu; = 0 nếu a = 0.
NK
2
H
6 tháng 9 2021
Nếu a,b cùng dấu thì \(\dfrac{a}{b}\ge0\)
Nếu a,b khác dấu thì \(\dfrac{a}{b}< 0\)
6 tháng 9 2021
\(\left[{}\begin{matrix}a\ge0,b>0\\a\le0,b< 0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\ge0\\ \left[{}\begin{matrix}a\ge0,b< 0\\a\le0,b>0\end{matrix}\right.\Rightarrow\dfrac{a}{b}\le0\)
HC
2
22 tháng 6 2015
Khi a;b cùng dấu thì a/b > 0
Khi a;b khác dấu thì a/b < 0
22 tháng 6 2015
+ Trong trường hợp a,b cùng dấu:
thì a/b >0 Vì thương của hai số nguyên cùng dấu là một số dương.
+ Trong trường hợp a,b khác dấu:
thì a/b>0 Vì thương của hai số nguyên khác dấu là một số âm.
V
2
25 tháng 8 2015
Khi a,b cùng dấu thì \(\frac{a}{b}\)>0 với a,b\(\ne\)0
Và a,b khác dấu thì \(\frac{a}{b}\)<0 với a,b\(\ne\)0
17 tháng 8 2017
Ta có:
(+):(+)=(+)
(-):(-)=(+)
(+):(-)=(-)
(-):(+)=(-)
Tự thao khảo nhé
PA
0
LH
2
TT
4
HZ
1 tháng 7 2016
Ta có :
Khi a, b cùng dấu :
Nếu a > 0 và b > 0 suy ra :
Nên : 
Nếu a < 0 và b < 0 suy ra :
Nên :
Khi a, b khác dấu :
Nếu a > 0 và b < 0 suy ra :
Nên : 
Nếu a < 0 và b > 0 suy ra :
Nên :
LM
1 tháng 7 2016
a, b cùng dấu thì a/b > 0 ..dễ hiểu thôi nếu cả a, b đều dương thì a/d dĩ nhiên dương, nếu cả a,b đều âm thì a/b cũng dương vì -a/-b = a/b (nhân hai vế với trừ 1)
a, b khác dấu thì a/b luôn âm nên a/b < 0
17 tháng 8 2017
Ta có:
(+):(+)=(+)
(-):(-)=(+)
(+):(-)=(-)
(-):(+)=(-)
Tự suy ra nhé
A và B cùng dấu nên AB>0
=>\(2x^3\cdot\left(-3\right)x^4>0\)
=>\(x^7< 0\)
=>x<0
có nhân 2 với -3 k ạ