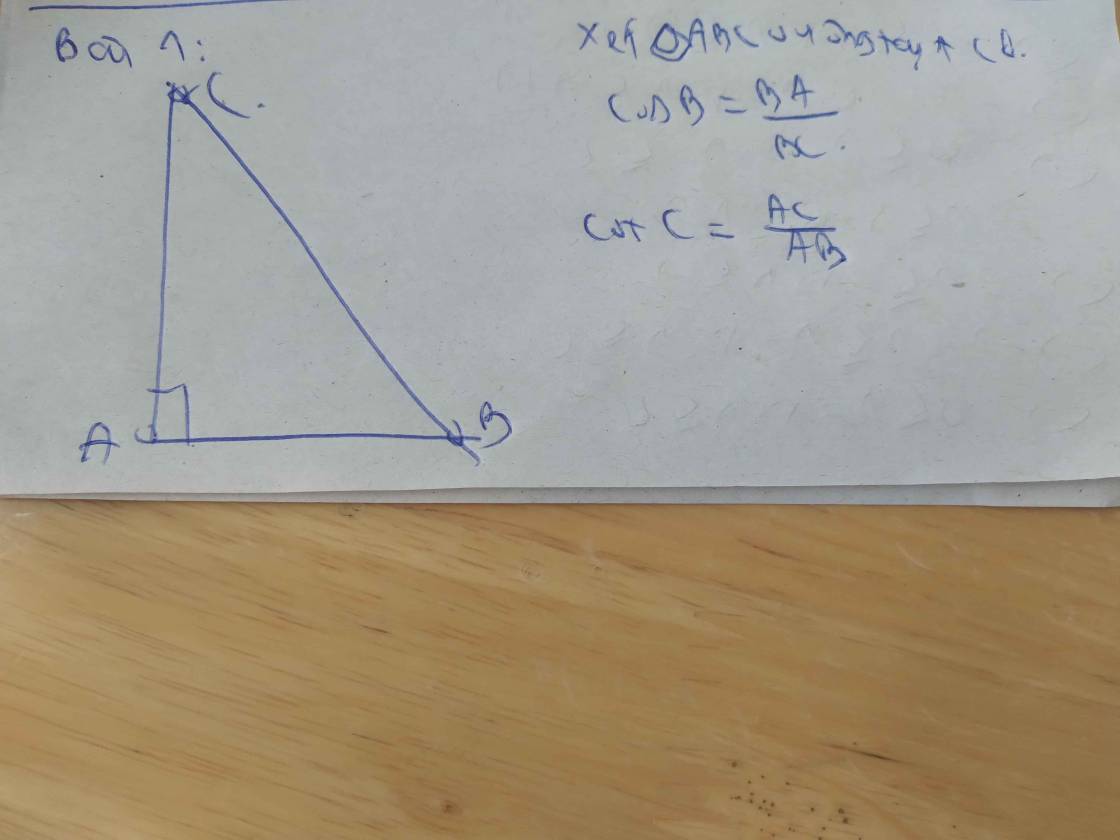
Cho tam giác ABC vuông tại A có góc B = α
a. Hãy viết các tỉ số lượng giác của góc nhọn α theo AB, AC, BC
b. Chứng minh: \(sin^2\alpha+cos^2\alpha=1\) ; \(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}\) ; \(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}\) ; \(\tan\alpha.\cot\alpha=1\)
c. Dùng kết quả của câu b để tính
A. \(\sin^2\alpha+2\cos^2\alpha\) biết sinα = \(\dfrac{1}{3}\)
B. \(\dfrac{sin35^o}{cos35^o}.\tan55^o+\dfrac{cos55^o}{sin55^o}.\cot35^o\)
C. \(cos^242^o+cos^253^o+cos^248^o+cos^237^o+cos^245^o\)
Em cảm ơn mng nhiều ạ!


Bài 2:
a: Xét ΔABC vuông tại A có
\(sin\alpha=sinB=\dfrac{AC}{BC}\)
\(cos\alpha=cosB=\dfrac{AB}{BC}\)
\(tan\alpha=tanB=\dfrac{AC}{AB}\)
\(cot\alpha=cotB=\dfrac{AB}{AC}\)
b: \(sin^2\alpha+cos^2\alpha=\left(\dfrac{AB}{BC}\right)^2+\left(\dfrac{AC}{BC}\right)^2\)
\(=\dfrac{AB^2+AC^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
\(tan\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{sin\alpha}{cos\alpha}\)
\(cot\alpha=\dfrac{AC}{AB}=\dfrac{AC}{BC}:\dfrac{AB}{BC}=\dfrac{cos\alpha}{sin\alpha}\)
c:
A: \(sin^2\alpha+cos^2\alpha=sin^2\left(\dfrac{1}{3}\right)+cos^2\left(\dfrac{1}{3}\right)=1\)
B: \(\dfrac{sin35^0}{cos35^0}\cdot tan55^0+\dfrac{cos55^0}{sin55^0}\cdot cot55^0\)
\(=\dfrac{cos55}{sin55}\cdot\dfrac{sin55^0}{cos55^0}+\dfrac{cos55^0}{sin55^0}\cdot tan55^0\)
=1+1
=2
C: \(cos^242^0+cos^253^0+cos^248^0+cos^237^0+cos^245^0\)
\(=\left(sin^242^0+cos^242^0\right)+\left(sin^237^0+cos^237^0\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)