cho tam giác abc có cạnh ab=25cm.trên cạnh bc lấy điểm m và n sao cho bm=2/3mn và nc=1/2 mn,biết đường cao mh của tam giác abm là 12 cm.tính diện tích tam giác abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Các bạn giải giúp mình với !28 tháng 12 2021
a) Diện tích tam giác ABC là:
\(\text{12 *10 :2= 60 (cm2)}\)
b) Diện tích tam giác AMB là:
\(\text{12 : 2 * 10 :2= 30 (cm^2)}\)
Diện tích tam giác AMC là:
\(\text{12 : 2 *10 :2= 30 (cm^2)}\)
Đáp số: a) 60 cm2
b) Bằng nhau
D
23 tháng 1 2022
a. Ta có: ▲ABC∼▲MNP (gt)
=>\(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{AH}{MQ}=k=\dfrac{1}{3}\) (với AH,MQ lần lượt là đường cao của tam giác ABC, MNP)
\(\dfrac{S_{ABC}}{S_{MNP}}=k^2=\dfrac{1}{9}\)
b. Ta có: \(\dfrac{P_{ABC}}{P_{MNP}}=\dfrac{1}{3}\)(cmt)=>PMNP=3PABC
*PMNP-PABC=60cm
=>3PABC-PABC=60cm
=>2PABC=60cm
=>PABC=30cm ; PMNP=90cm
c. Ta có: \(\dfrac{S_{ABC}}{S_{MNP}}=\dfrac{1}{9}\)(cmt)=>SMNP=9SABC
*SMNP+SABC=640cm2
=>9SABC+SABC=640cm2
=>10SABC=640cm2
=>SABC=64cm2 ; SMNP=576cm2
29 tháng 11 2023
\(HB+HC=BC\)
=>\(\dfrac{1}{3}HC+HC=BC\)
=>\(BC=\dfrac{4}{3}HC\)
mà \(HB=\dfrac{1}{3}HC\)
nên \(\dfrac{BC}{HB}=\dfrac{4}{3}:\dfrac{1}{3}=4\)
=>BC=4HB
=>\(S_{ABC}=4\cdot S_{AHB}=4\cdot6=24\left(cm^2\right)\)
CM
26 tháng 12 2017
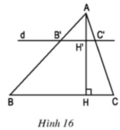
a) Theo hệ quả định lý Ta let ta có:
ΔABC có B’C’ // BC (B’ ∈ AB; C’ ∈ AC) ⇒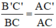 
ΔAHC có H’C’ // HC (H’ ∈ AH, C’ ∈ AC) ⇒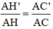 
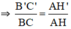
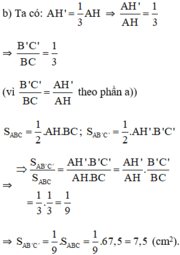
BM+MN+NC=BC
=>\(BC=MN+\dfrac{2}{3}MN+\dfrac{1}{2}MN=\dfrac{13}{6}MN\)
=>\(\dfrac{BM}{BC}=\dfrac{2}{3}:\dfrac{13}{6}=\dfrac{2}{3}\cdot\dfrac{6}{13}=\dfrac{12}{39}=\dfrac{4}{13}\)
=>BC=3,25BM
\(S_{ABM}=\dfrac{1}{2}\cdot MH\cdot AB=\dfrac{1}{2}\cdot12\cdot25=150\left(cm^2\right)\)
BC=3,25BM nên \(S_{ABC}=3,25\cdot S_{ABM}=3,25\cdot150=487,5\left(cm^2\right)\)