y×6/11+y×5/11=2025
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 8 2023
\(y\times\dfrac{6}{11}+y\times\dfrac{5}{11}=2025\)
\(y\times\left(\dfrac{5}{11}+\dfrac{6}{11}\right)=2025\)
\(y\times1=2025\)
\(y=2025\)
14 tháng 8 2023
\(y.\dfrac{6}{11}+y.\dfrac{5}{11}=2025\)
\(y.\left(\dfrac{6}{11}+\dfrac{5}{11}\right)=2025\)
\(y.\left(\dfrac{11}{11}\right)=2025\)
\(y=2025\)
Dấu . là dấu nhân
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
31 tháng 7 2023
\(Y\times6+11\times\dfrac{5}{11}=2025\\ Y\times6+5=2025\\ Y\times6=2025-5\\ Y\times6=2020\\ Y=\dfrac{2020}{6}\\ Y=\dfrac{1010}{3}\)
31 tháng 7 2023
\(y\times6+11\times\dfrac{5}{11}=2025\\ y\times6+5=2025\\y\times6=2025-5\\ y\times6=2020\\ y=2020:6\\ y=\dfrac{1010}{3}\)
NL
1
AH
Akai Haruma
Giáo viên
30 tháng 11 2021
Lời giải:
ĐKXĐ: $x\geq 0; y\geq 1; z\geq 2$
PT \(\Leftrightarrow (x-2\sqrt{x}+1)+[(y-1)-4\sqrt{y-1}+4]+[(z-2)-6\sqrt{z-2}+9]=0\)
\(\Leftrightarrow (\sqrt{x}-1)^2+(\sqrt{y-1}-2)^2+(\sqrt{z-2}-3)^2=0\)
Vì \((\sqrt{x}-1)^2, (\sqrt{y-1}-2)^2, (\sqrt{z-2}-3)^2\geq 0\) nên để tổng của chúng bằng $0$ thì:
\((\sqrt{x}-1)^2=(\sqrt{y-1}-2)^2=(\sqrt{z-2}-3)^2=0\)
$\Leftrightarrow x=1; y=5; z=11$
31 tháng 12 2023
a: \(\sqrt{x^2+6x+9}=\sqrt{11+6\sqrt{2}}\)
=>\(\sqrt{\left(x+3\right)^2}=\sqrt{\left(3+\sqrt{2}\right)^2}\)
=>\(\left|x+3\right|=\left|3+\sqrt{2}\right|=3+\sqrt{2}\)
=>\(\left[{}\begin{matrix}x+3=3+\sqrt{2}\\x+3=-3-\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{2}\\x=-6-\sqrt{2}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}2x-y=4\\x+2y=-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-2y=8\\x+2y=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y+x+2y=8-3\\2x-y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=5\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\cdot1-4=-2\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 3 2023
\(\left\{{}\begin{matrix}x-y=-9\\x+y=11\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2x=2\\x+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=11-x=10\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
30 tháng 3 2023
Giải hệ phương trình:
\(\left\{{}\begin{matrix}x-y=-9\\x+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\-9+y+y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\2y-9=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+y\\2y=20\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-9+10\\y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=10\end{matrix}\right.\)
PT
1
6 tháng 3 2021
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
PT
1
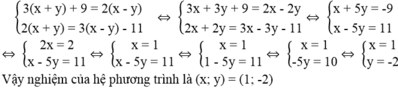
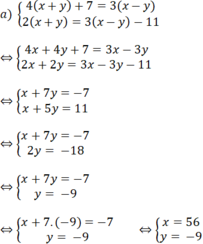
y × 6/11 + y × 5/11 =2025
y × (6/11+5/11) =2025
y ×1 =2025
y =2025
y × 6/11 + y × 5/11 =2025
y × (6/11+5/11) =2025
y ×1 =2025
y =2025