Cho tam giác abc (góc a bằng 90 độ), kẻ AH vuông góc với BC, kẻ HB vuông góc với AB và kéo dài để có PE=PH. Kẻ HQ vuông góc với AC và kéo dài để có QF =QH.
a) CM: tam giác APE= tam giác APH. và tam giác AQG = tam giác AQF
b) CM: 3 điểm E, A, F thẳng...
Đọc tiếp
Cho tam giác abc (góc a bằng 90 độ), kẻ AH vuông góc với BC, kẻ HB vuông góc với AB và kéo dài để có PE=PH. Kẻ HQ vuông góc với AC và kéo dài để có QF =QH.
a) CM: tam giác APE= tam giác APH. và tam giác AQG = tam giác AQF
b) CM: 3 điểm E, A, F thẳng hàng.
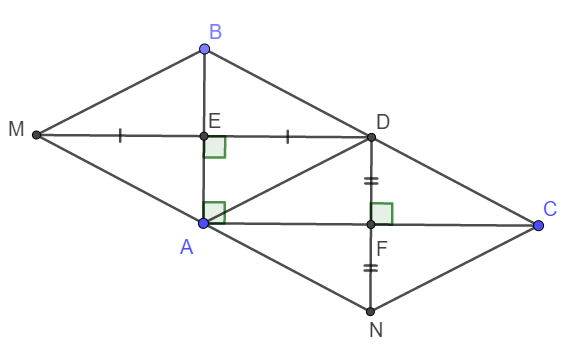
a: Xét ΔAPE vuông tại P và ΔAPH vuông tại P có
AP chung
PE=PH
Do đó: ΔAPE=ΔAPH
Xét ΔAQH vuông tại Q và ΔAQF vuông tại Q có
AQ chung
QH=QF
Do đó; ΔAQH=ΔAQF
b: ΔAPE=ΔAPH
=>\(\widehat{PAE}=\widehat{PAH}\)
=>AP là phân giác của góc HAE
ΔAQH=ΔAQF
=>\(\widehat{QAH}=\widehat{QAF}\)
=>AQ là phân giác của góc HAF
\(\widehat{EAF}=\widehat{EAH}+\widehat{FAH}\)
\(=2\widehat{QAH}+2\cdot\widehat{PAH}=2\cdot\left(\widehat{QAH}+\widehat{PAH}\right)\)
\(=2\cdot\widehat{QAP}=180^0\)
=>E,A,F thẳng hàng