Cho tam giác ABC có \(\widehat{B}\) = \(80^o\), \(\widehat{C}\) = \(90^o\) . Tia phân giác của góc A cắt BC ở D . Tính \(\widehat{ADC}\) ,\(\widehat{ADB}\) .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
20 tháng 4 2017
\(\widehat{BAC}\)= 1800 - (\(\widehat{B}+\widehat{C}\)) = 1800 - ( 800 + 300)= 700
\(\widehat{A}_1\)=\(\widehat{A}_2\)=\(\dfrac{\widehat{A}}{2}\)=\(\dfrac{70^0}{2}\)= 350
\(\widehat{ADC}=\widehat{B}+\widehat{A}_1\)(Góc ngoài của tam giác)
=800 + 350)= 1150
Do đó \(\widehat{ADB}\)= 1800 - \(\widehat{ADC}\)= 1800 + 1150=650
20 tháng 4 2017
Hình vẽ: 
Gọi A1, A2 là 2 góc được tạo ra bởi tia phân giác góc A.
Ta có:
Góc ∠BAC = 1800 – ( ∠B + ∠C)
= 1800 – ( 800 + 300) = 700
Hay ta có thể gọi ∠A = 700
Góc ∠A1 = ∠A2
= ∠A/2 = 700 /2 = 350
- Xét tam giác ADC ta có: Góc ∠ADC = 1800 – (∠C + ∠A2)
= 1800 – (350 + 300)= 1150
- Do đó góc ∠ADB = 1800 – ∠ADC
= 1800 – 1150
= 650
PC
16 tháng 9 2016
Trần Nguyễn Hoài Thư
Bạn tự vẽ hình ( hình dễ lắm nhé )
Giải
Xét \(\Delta ABC\) có :
\(\widehat{BAC}+\widehat{CBA}+\widehat{ACB}=180^O\)
\(\Rightarrow\widehat{BAC}=180^O-80^O-30^O\)
\(\Rightarrow\widehat{BAC}=70\)
Ta có : AD là tia phân giác của \(\widehat{BAC}\)
\(\Rightarrow\widehat{BAD}=\widehat{DAC}=\frac{70^O}{2}=35^O\)
Xét \(\Delta ABD\) có :
\(\widehat{ABD}+\widehat{BAD}+\widehat{BDA}=180^O\)
\(\Rightarrow\widehat{ADB}=180^O-35^O-80^O=65^O\) ( Vì \(\widehat{BAD}=35^O;\widehat{ABD}=80^O\) (CMT )
CMTT ta có :
\(\widehat{ADC}=180^O-30^O-35^O=115^O\)
Vậy \(\widehat{ADC}=115^O\) và \(\widehat{ADB}=65^O\)
Chúc bạn học tốt 
VC
11 tháng 1 2018
Ta có :
A+B+C=180(tính chất của một tam giác)
⇒A=180-B-C
⇒A=180-20
⇒A=160
vì tia phân giác của góc A cắt BC tại D nên A1=A2=\(\dfrac{160}{2}\)=80
\(\Leftrightarrow\)D1=80
Vì góc D1 và góc D2 là 2 góc kề bù nên D1+D2=180
mà góc D1=80
\(\Rightarrow\)D2=180-80
\(\Rightarrow\)D2=100
Vay : D1=80, D2=100
mk ko viết đc kí hiệu góc và độ mong mọi người thông cảm
17 tháng 9 2023
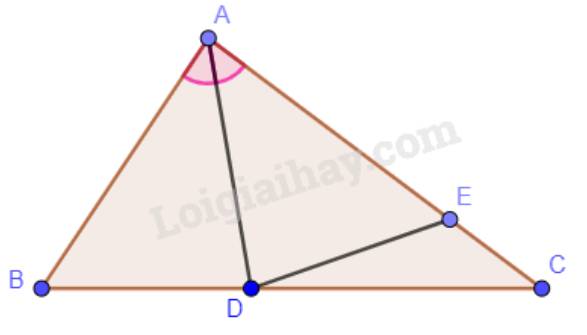
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
5 tháng 10 2023
a) Để chứng minh a) ta cần chứng minh rằng góc ADC bằng góc BEC.
Vì AD là đường phân giác của góc BAC, nên ta có:
∠DAB = ∠DAC (1)
Tương tự, vì BE là đường phân giác của góc ABC, nên ta có:
∠CBA = ∠CBE (2)
Từ (1) và (2), ta có:
∠DAB + ∠CBA = ∠DAC + ∠CBE
∠DAB + ∠CBA = ∠BAC + ∠ABC
∠DAB + ∠CBA = ∠ABC + ∠BAC
Do đó, góc ADC bằng góc BEC.
Tiếp theo, để chứng minh rằng góc A bằng góc B, ta sử dụng định lý phụ của đường phân giác:
∠DAB = ∠DAC
∠EBA = ∠EBC
Vì ∠ADC = ∠BEC (đã chứng minh ở trên), nên ta có:
∠DAC + ∠ADC = ∠DAB + ∠ABC
∠DAB + ∠ABC = ∠DAC + ∠ADC
Từ đây, suy ra ∠A = ∠B.
Vậy, điều phải chứng minh a) đã được chứng minh.
b) Để chứng minh b), ta cần chứng minh rằng góc ADB bằng góc BEC.
Từ ∠ADB = ∠BEC (đã chứng minh ở a)), ta có:
∠ADB + ∠BEC = ∠BEC + ∠BEC
∠ADB + ∠BEC = 2∠BEC
∠ADB = ∠BEC
Do đó, góc ADB bằng góc BEC.
Tiếp theo, ta có:
∠A + ∠B + ∠C = 180° (định lý tổng các góc trong tam giác)
∠ADB + ∠B + ∠BEC = 180°
∠BEC + ∠B + ∠BEC = 180° (vì ∠ADB = ∠BEC)
2∠BEC + ∠B = 180°
2∠BEC = 180° - ∠B
∠BEC = (180° - ∠B) / 2
∠BEC = 90° - ∠B/2
∠BEC = 90° - ∠A/2 (vì ∠A = ∠B)
∠A/2 + ∠B/2 + ∠C = 90°
∠A/2 + ∠B/2 + ∠C = 90° - ∠A/2
∠A/2 + ∠A/2 + ∠C = 90° - ∠A/2
∠A + ∠C = 90° - ∠A/2
∠A + ∠C + ∠A/2 = 90°
2∠A + ∠C = 180°
∠A + ∠C = 180° - ∠A
∠A + ∠C = ∠B
∠A + ∠B + ∠C = 180°
∠A + ∠B + ∠C = 120° + 60°
∠A + ∠B + ∠C = 180°
Do đó, ∠A + ∠B = 120°.
Vậy, điều phải chứng minh b) đã được chứng minh.
Sai thì thôi nhá! Đừng có chọn sai! : | :v
Giải
Ta có hình vẽ:
Ta có : Góc C > D và lớn hơn : 900 - 80o = 100
\(\Rightarrow\widehat{bAc}=10^o\)
Nhận xét: Tia phân giác chia tam giác thành hai phần bằng nhau.
\(\Rightarrow2_p=10^o:2=5^o\) ( 2p là hai phần nha)
\(\Rightarrow\widehat{aDc}=90^o-5^o=85^o\)
\(\Rightarrow\widehat{aDb}=80^o-5^o=75^o\)
Ai giúp mình thì làm cách giải chi tiết nha