Viết giả thiết, kết luận và chứng minh định lí sau: Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong không bằng nhau thì hai đường thẳng đó cắt nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 7 2017
Đáp án B
Gỉa thiết của định lí trên là a / / b ; c ∩ a = A ; c ∩ b = B
29 tháng 10 2016
A B x y C 1 1
\(\widehat{xAB}+\widehat{yBA}=180^0\)(2 góc trong cùng phía của Ax // By)
mà\(\widehat{A_1}=\frac{\widehat{xAB}}{2};\widehat{B_1}=\frac{\widehat{yBA}}{2}\)(AC,BC là phân giác của\(\widehat{xAB};\widehat{yBA}\))
=>\(\Delta ABC\)có :\(\widehat{A_1}+\widehat{B_1}=\frac{\widehat{xAB}+\widehat{yBA}}{2}=\frac{180^0}{2}=90^0\)\(\Rightarrow\Delta ABC\)vuông tại C hay AC _|_ BC
8 tháng 10 2015
GT: 1 đt cắt 2 đường thẳng...sole trong=nhau
Kl:2đt đó //
b)Gt:1đt cắt 2 đt//
Kl:2 góc sole trong=nhau
29 tháng 9 2018
- Gỉa thiết: Một đường thẳng cắt 2 đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau
- Kết luận: Các góc đồng vị bằng nhau
29 tháng 9 2018
giả thiết luôn luôn đứng trước chữ thì còn kết luận sẽ đứng sau chữ thì ok bạn vẽ hình ra tìm đâu là cặp góc SlT rồi chứng minh nó bằng nhau thì ta suy ra đc các góc đồng vị bằng nhau trong sách hình như có hướng dẫn mà
30 tháng 9 2017
Cho định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong số các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau
- Hãy cho biết giả thuyết của định lí đó
- Hãy cho biết kết luận của định lí đó
- Hãy chứng minh định lí đó
Được cập nhật Hôm qua lúc 20:29
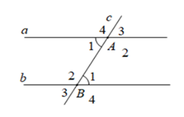
a cắt b tại A, a cắt c tại B
\(\widehat{A_1}\ne\widehat{B_2}\)
Vì \(\widehat{A_1}\ne\widehat{B_2}\)
nên b sẽ không song song với c
mà b và c là hai đường thẳng phân biệt
nên b cắt c