tìm giá trị nhỏ nhất B= 2x^2 - 5x + 6
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
18 tháng 11 2017
đổi 2m 3dm = 23dm;43m = 430 dm.
ta có: 430 : 23 =18( dư 16 dm )
đổi 16dm = 1,6 m
vậy với 43m vải sẽ may được 18 bộ quần áo và còn thừa 1,6m vải.
NP
1
KN
11 tháng 10 2019
\(B=2x^2-5x+3\)
\(=2\left(x^2-\frac{5}{2}x+\frac{3}{2}\right)\)
\(=2\left(x^2-\frac{5}{2}x+\frac{25}{16}-\frac{1}{16}\right)\)
\(=2\left[\left(x-\frac{5}{4}\right)^2-\frac{1}{16}\right]\)
\(=2\left[\left(x-\frac{5}{4}\right)^2\right]-\frac{1}{32}\ge\frac{-1}{32}\)
A
11 tháng 10 2019
\(B=2x^2-5x+3\)
\(=2\left(x^2-\frac{5}{2}x+\frac{3}{2}\right)\)
\(=2\left(x^2-\frac{5}{4}\cdot2x+\left(\frac{5}{4}\right)^2-\left(\frac{5}{4}\right)^2+\frac{3}{2}\right)\)
\(=2\left[\left(x-\frac{5}{4}\right)^2-\frac{25}{16}+\frac{3}{2}\right]\)
\(=2\left[\left(x-\frac{5}{4}\right)^2-\frac{1}{16}\right]\)
\(=2\left(x-\frac{5}{4}\right)^2-\frac{1}{8}\)
có\(2\left(x-\frac{5}{4}\right)^2\ge0\)
\(\Rightarrow\left(x-\frac{5}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\)
\(\Rightarrow GTNNB=-\frac{1}{8}\)
với \(\left(x-\frac{5}{4}\right)^2=0;x=\frac{5}{4}\)
16 tháng 6 2017
a) Để A= I 2x-3 I + 1/2 bé nhất thì I 2x-3 I phải bé nhất, mà I 2x-3 I bé hơn hoặc = 0=> I2x-3 I =0 => 2x=3=> x=3/2
Vậy giá trị nhỏ nhất của A là 1/2 tại x= 3/2
b) Để B nhỏ nhất thì | 5x + 6 | phải nhỏ nhất, mà | 5x + 6 | bé hơn hoặc = 0=> | 5x + 6 |=0 => x= -6/5
Vậy giá trị nhỏ nhất của B là -0.25 tại x=-6/5
c) Để C nhỏ nhất thì Ix-3I hoặc I x+7I phải nhỏ nhất, mà I x-3 I và Ix-7I bé hơn hoặc = 0 => x-3 = 0 hoặc x+7 = 0
=> x=3 hoặc x= -7
Thay x=3 vào C, có: | 3- 3 | + | 3 + 7 | = 0+ 10 = 10
Thay x=7 vào C, có: | -7 - 3 | + | -7 + 7 | = 10+0 = 10
=> giá trị nhỏ nhất của C là 10 tại x=3 hoặc x=7
HV
3
GB
1
KV
20 tháng 3 2023
A = 5x² + 6
Do x² ≥ 0
⇒ 5x² ≥ 0
⇒ 5x² + 6 ≥ 6
Vậy giá trị nhỏ nhất của A là 6 khi x = 0
--------------------
B = 4(2x - 4)² + 2023
Do (2x - 4)² ≥ 0
⇒ 4(2x - 4)² ≥ 0
⇒ 4(2x - 4)² + 2023 ≥ 2023
Vậy giá trị nhỏ nhất của B là 2023 khi x = 2
T
8 tháng 9 2023
\(a,x^2+3x+9\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
Ta thấy: \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
\(b,2x^2-5x+10\)
\(=2x^2-5x+\dfrac{25}{8}+\dfrac{55}{8}\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{55}{8}\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\)
Ta có: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{4}\)
#\(Toru\)
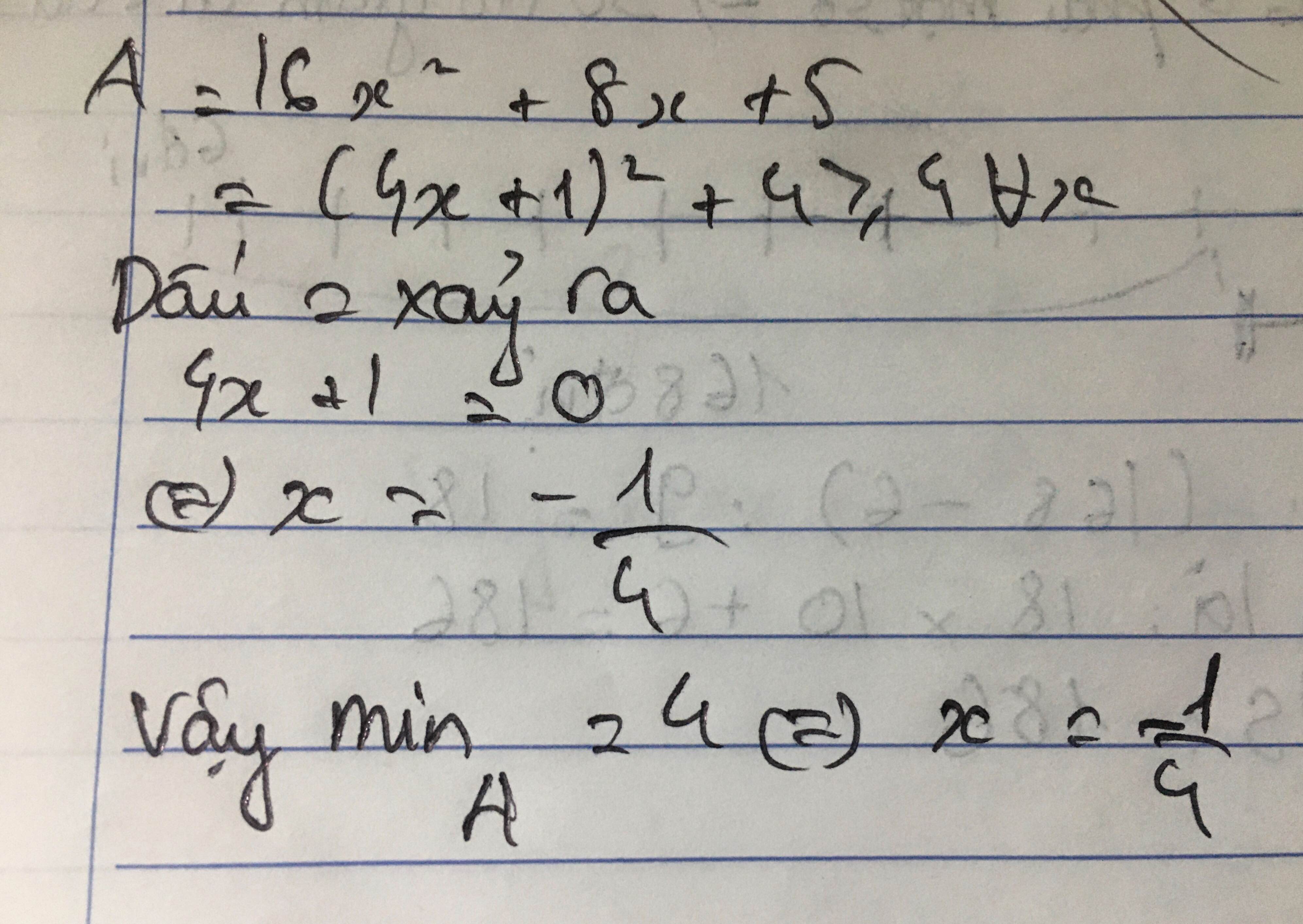
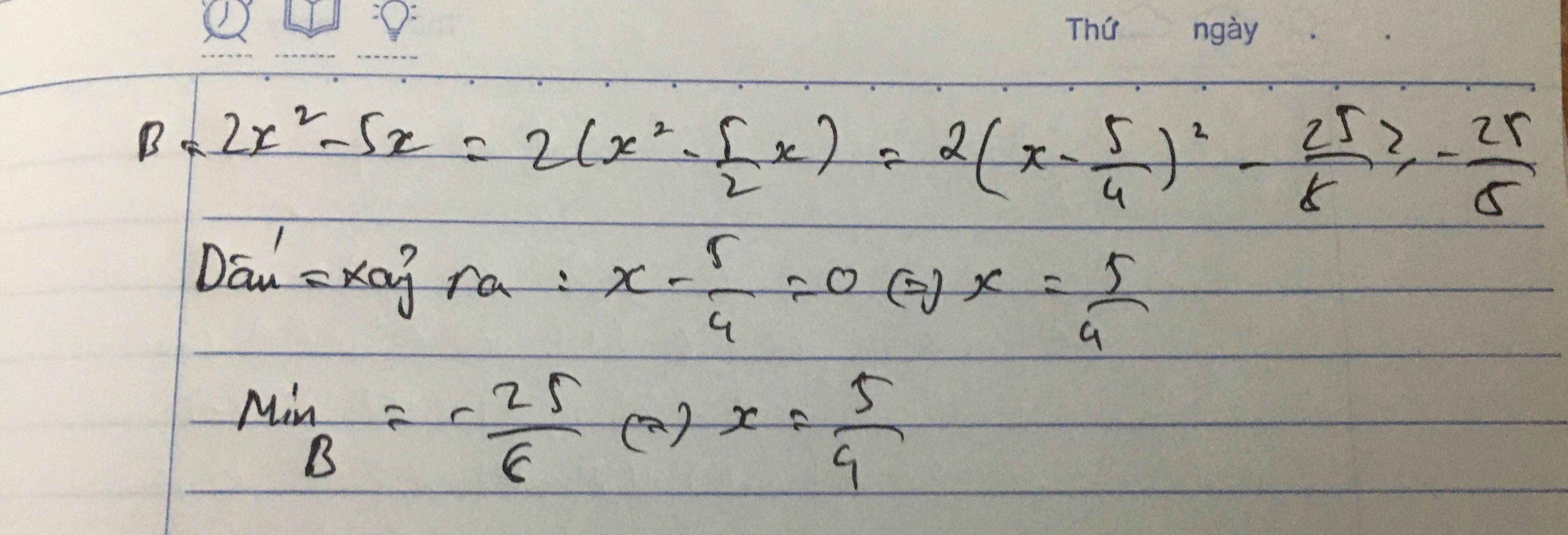
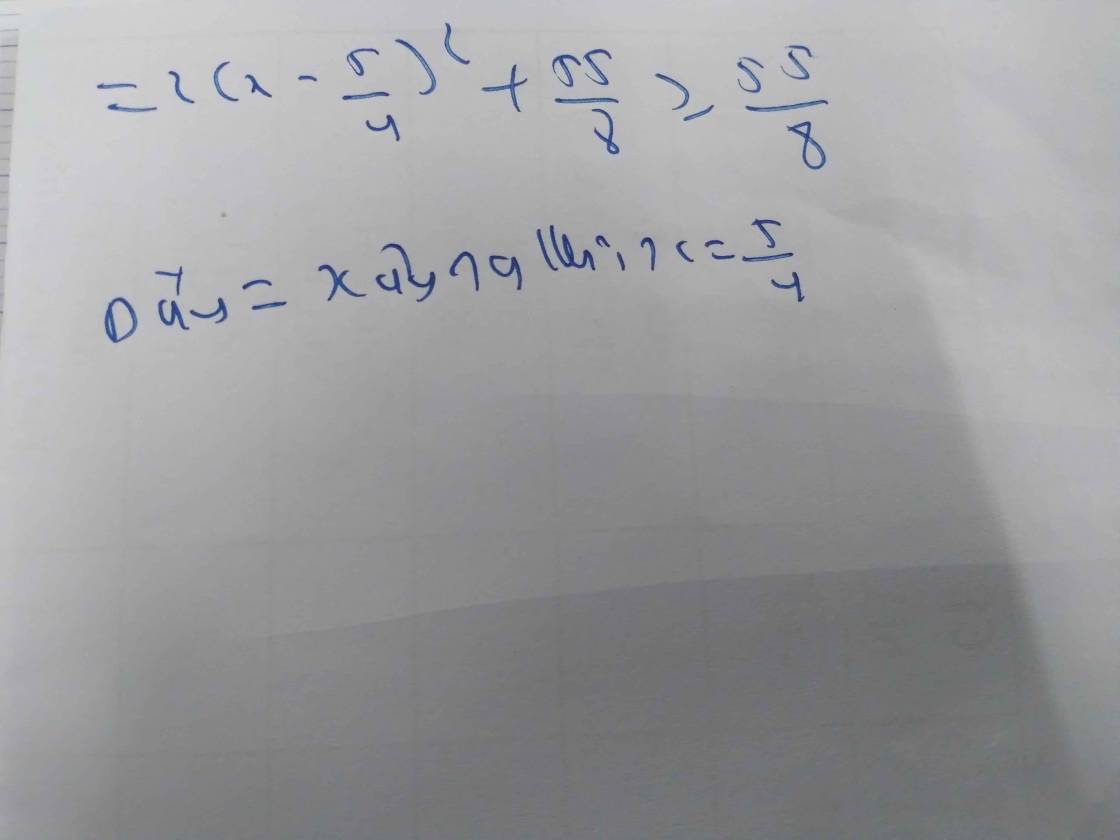
\(B=2x^2-5x+6\\ =2\left(x^2-\dfrac{5}{2}x+3\right)\\ =2\left[\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{23}{16}\right]\\ =2\left(x-\dfrac{5}{4}\right)^2+\dfrac{23}{8}\)
Ta có: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x=>B=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{23}{8}\ge\dfrac{23}{8}\forall x\)
Dấu "=" xảy ra: `x-5/4=0<=>x=5/4`
sai nhé