cho tam giác ABC vuông tại A , AH vuông góc với BC . trên tia đối của tia HA lấy M sao cho HM=HA . chứng minh EM vuông góc với AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 12 2021
a: Xét ΔABE và ΔACE có
AB=AC
AE chung
BE=CE
Do đó: ΔABE=ΔACE
12 tháng 1 2022
a: Xét ΔAHB vuông tại H và ΔAHK vuông tại H có
AH chung
HB=HK
Do đó: ΔAHB=ΔAHK
b: Ta có; ΔAHB=ΔAHK
nên \(\widehat{HAK}=\widehat{BAH}\)
mà \(\widehat{BAH}=\widehat{EHA}\)
nên \(\widehat{EHA}=\widehat{HAK}\)
30 tháng 8 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{60}{13}\left(cm\right)\)
b: Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
8 tháng 3 2023
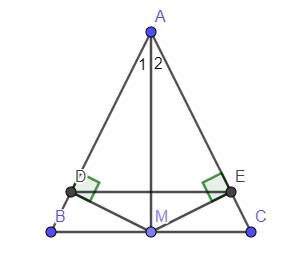
`a)`
Xét `Delta ABM` và `Delta ACM` có :
`{:(AB=AC(GT)),(AM-chung),(BM=CM(M là tđ BC)):}}`
`=>Delta ABM=Delta ACM(c.c.c)(đpcm)`
`b)`
`Delta ABM=Delta ACM(cmt)=>hat(A_1)=hat(A_2)`
mà `AM` nằm giữa `AB` và `AC`
nên `AM` là p/g của `hat(BAC)(đpcm)`
`c)`
Xét `Delta ADM` và `Delta AEM` có :
`{:(hat(ADM)=hat(AEM)(=90^)),(AM-chung),(hat(A_1)=hat(A_2)(cmt)):}}`
`=>Delta ADM=Delta AEM(ch-gn)`
`=>AD=AE` ( 2 cạnh t/ứng )
`=>Delta ADE` cân tại `A(đpcm)`
12 tháng 12 2021
a: Xét ΔABE và ΔACE có
AB=AC
AE chung
BE=CE
Do đó: ΔABE=ΔACE
20 tháng 2 2019
Nè sai đề phải k PK vuông góc vs chứ ko phải PH là 1
I đâu ra mà c/m hai góc đó là 2 nêu đề /m HPB và KPC thì làm đc
Nếu đề sai thì viết vào dưới bài này mình sẽ giải cho
30 tháng 4 2022
a: Xet ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
AF=AE
Do đó: ΔAFM=ΔAEM
Suy ra: \(\widehat{BAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc BAC
12 tháng 3 2022
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm
16 tháng 3 2022
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
\(\widehat{MAH}=\widehat{NAH}\)
Do đó: ΔAMH=ΔANH
Suy ra: AM=AN
hay ΔAMN cân tại A
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC